一、概念
散列表: 根据给定的关键字来计算出关键字在表中的地址的数据结构。也就是说,散列表建立了 关键字 和 存储地址 之间的一种直接映射关系,
**散列函数:**一个把查找表中的关键字映射成该关键字对应的地址的函数,记为:Hash(key)=Addr。
散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为“冲突”,这些发生碰撞的不同关键字称为 同义词 。

二、散列函数和冲突的处理方法
构造散列函数的tips:
- 散列函数的定义域必须包含 全部需要存储的关键字 ,而值域的范围则依赖于散列表的大小或地址范围。 > + 散列函数计算出来的地址应该能 等概率、均匀地 分布在整个地址空间,从而减少冲突的发生。 > + 散列函数应尽量简单,能够在较短的时间内就计算出任一关键字对应的散列地址。
三、常用Hash函数的构造方法
**1.直接定址法:**直接取关键字的某个线性函数值为散列地址,散列函数为H(key)=a X key + b。式中,a和b是常数、这种方法计算最简单,并且不会产生冲突
**2.除留余数法:**假定散列表表长为m,取一个不大于m但最接近或等于m的质数p, 利用以下公式把关键字转换成散列地址。散列函数为H(key)=key%p
除留余数法的关键是选好p,使得每一个关键字通过该函数转换后等概率地映射到散列空间上的任一地址,从而尽可能减少冲突的可能性
**3.数字分析法:**设关键字是r进制数(如十进制数),而r个数码在各位上出现的频率不一定相同,可能在某些位上分布均匀些,每种数码出现的机会均等;而在某些位上分布不均匀,只有某几种数码经常出现,则应选取数码分布较均匀的若干位作为散列地址。这种方法适合于已知的关键字集合。

4.平方取中法
顾名思义,取关键字的平方值的中间几位作为散列地址。具体取多少位要看实际情况而定。这种方法得到的散列地址与关键字的每一位都有关系,使得散列地址分布比较均匀。

5.折叠法
将关键字分割成位数相同的几部分(最后一部分的位数可以短一些),然后取这几部分的叠加和作为散列地址,这种方法称为叠加法。关键字位数很多,而且关键字中每一位上数字分布大致均匀时,可以采用折叠法得到散列地址。

常用Hash函数的冲突处理办法:
**1.开放定址法:**将产生冲突的Hash地址作为自变量,通过某种冲突解决函数得到一个新的空闲的Hash地址。
1.1 线性探测法:冲突发生时,顺序查看表中下一个单元(当探测到表尾地址m-1时,下一个探测地址是表首地址0),直到找出一个空闲单元(当表未填满时一定能找到一个空闲单元)或查遍全表。

线性探测法会造成大量元素在相邻的散列地址上“聚集”(或堆积)起来,大大降低查找效率。
1.2 平方探测法:设发生冲突的地址为d,平方探测法得到的新的地址序列为d+1平方,d-1平方,d+2平方,d-2平方......平方探测法是一种较好的处理冲突的方法,可以避免出现“堆积”问题,它的缺点是不能探测到散列表上的所有单元,但至少能探测到一半单元。

1.3 再散列法:又称为双散列法。需要使用两个散列函数,当通过第一个散列函数H(Key)得到的地址发生冲突时,则利用第二个散列函数Hash2(Key)计算该关键字的地址增量。

Hi=(H(Key)+i*Hash2(Key))%m 其中m是散列表长,i是冲突次数,初值为0
比如现在散列表中插入19,H(key)=19 Mod 8=3,产生第一次冲突,i=1, 带入Hi计算Hi(3+1*1)%9=4,于是19插入到下标为4的位置。
1.4 伪随机序列法:当发生地址冲突时,地址增量为伪随机数序列,称为伪随机序列法。
**2.拉链法:**对于不同的关键字可能会通过散列函数映射到同一地址,为了避免非同义词发生冲突,可以把所有的同义词存储在一个现行链表中,这个线性链表由散列地址唯一标识。拉链法适用于经常进行插入和删除的情况。
**3.散列表的查找过程:**类似于构造散列表,给定一个关键字Key。
先根据散列函数计算出其散列地址。然后检查散列地址位置有没有关键字。
(1)如果没有,表明该关键字不存在,返回查找失败。
(2)如果有,则检查该记录是否等于关键字。
①. 如果等于关键字,返回查找成功。
②. 如果不等于,则按照给定的冲突处理办法来计算下一个散列地址,再用该地址执行上述过程。
**4.散列表的查找性能:**和装填因子有关。
装填因子:散列表的装填因子一般记为α,定义为一个表的装满程度。
计算方法为α=表中记录数n/散列表长度m
散列表的平均查找长度依赖于散列表的装填因子α,而不直接依赖于n或m。
α越大,表示装填的记越“满”,发生冲突的可能性就越大,反之发生冲突的可能性越小。
三、练习题
题目
已知一组关键字为{26,36,41,38,44,15,68,12,6,51,25},用链地址法解决冲突,假设装填因子α=0.75,Hash函数的形式为H(key)=key%P,回答以下问题: > > (1)构造出Hash函数。 > > (2)分别计算出等概率情况下查找成功和查找失败的平均查找长度。(查找失败的计算中只将与关键字的比较次数计算在内即可)
(1)由α=表中记录数n/散列表长度m,此时n=11,α=0.75,所以m=[11/0.75]=15
由于采用除留取余法,根据除留取余法Hash函数的选择要求, P应该取不大于表长的最大素数 ,所以P=13。
所以Hash函数为H(key)=key%13
(2)先求出各个关键字根据Hash函数计算得到的散列地址

画出链地址法解决冲突的示意图

由于表中只有11个关键字,所以查找成功的情况必定是这11个关键字。 计算方法就是水平来看每一行有多少个关键字。
ASL(成功)=(1*7+2*2+3*1+4*1)/11=18/11
查找失败的情况包括整个散列表的情况,一共有13种
题目注明仅计算与关键字的比较次数
以地址为2为例,查找失败要先检查41,再检查15,两次之后发现查找失败
ASL(失败)=(1+0+2+1+0+1+1+0+0+0+1+0+4)/13=11/13
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
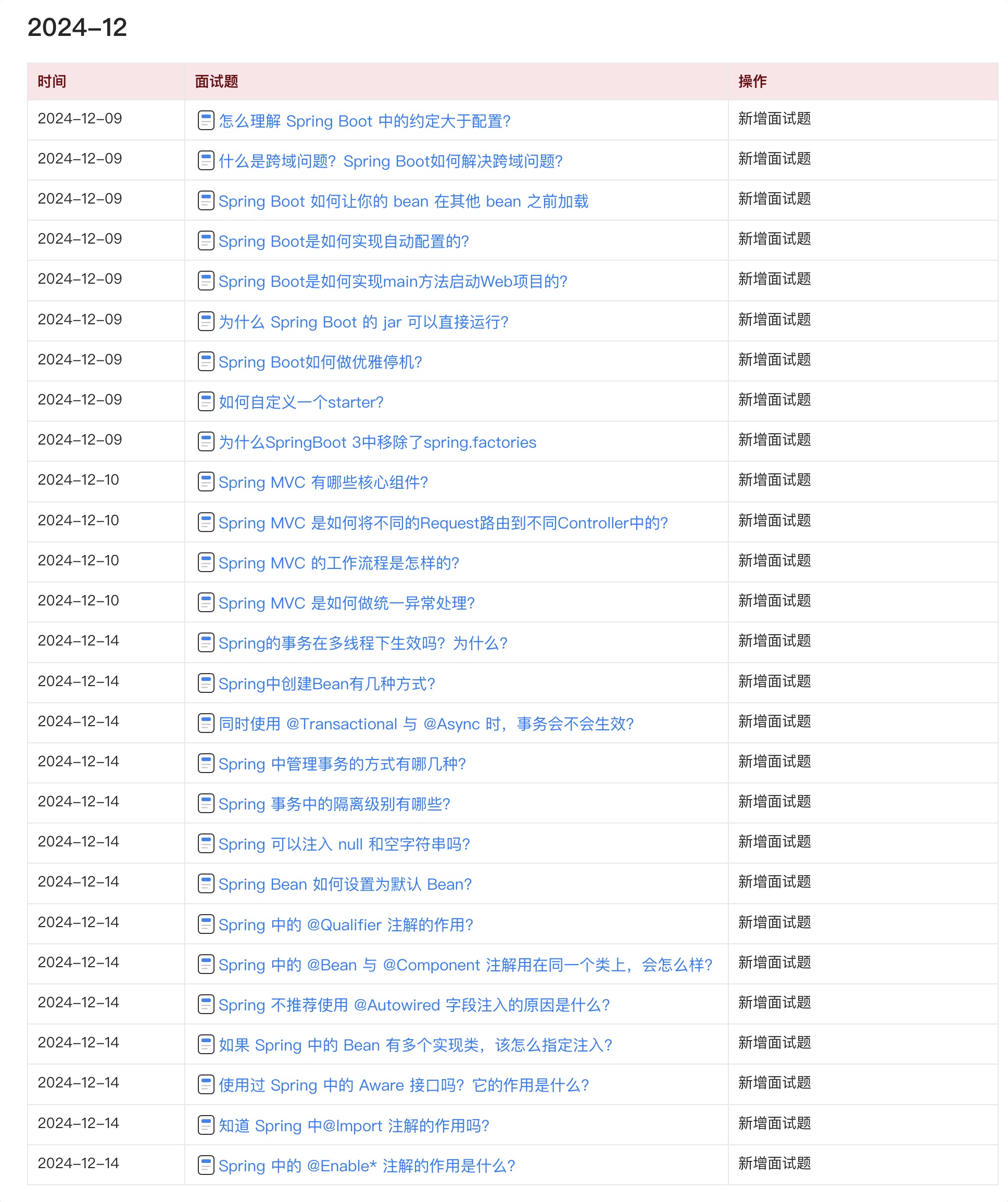
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

