查找
基本概念
查找就是在数据集中找出一个“特定元素”。
查找表是由同一类型的数据元素(或记录)构成的集合。
查找表是一种以集合为逻辑结构、以查找为核心的数据结构。
关键字
有时候我们需要指定某数据项的值来查找，这就用到了关键字。
关键字是数据元素中某个数据项的值，用以标识一个数据元素。
若此关键字可以识别唯一的一个记录，则称之谓“主关键字”；若此关键字能识别若干记录，则称之谓“次关键字”。
例：
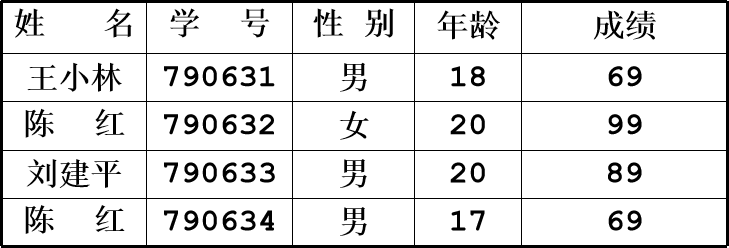
对查找表经常进行的操作:
1）查询某个“特定的”数据元素是否在查找表中；
2）检索某个“特定的”数据元素的各种属性；
3）在查找表中插入一个数据元素；
4）从查找表中删去某个数据元素。
查找表可分为 两类 :
静态查找 ：仅作查询和检索操作。查找前后查找表未发生变化。
动态查找 ：在查询之后，将 “不在查找表中”的数据元素插入到查找表中；或者，从查找表中删除“在查找表中”的数据元素。 查找前后查找表发生了变化。
采用何种查找方法，取决于使用哪种数据结构来表示“查找表”。即表中记录是按何种方式组织的，根据不同的数据结构采用不同的查找方法。
平均查找长度:
查找算法中的基本运算是记录的关键字与给定值所进行的比较。其执行时间通常取决于关键字的比较次数，也称为平均查找长度ASL 。
ASL是衡量一个查找算法优劣的重要指标。
定义为：
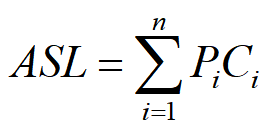
n 是查找表中记录的个数
Pi 是查找第i个记录的概率
Ci 是找到第i个记录所需进行的比较次数。
静态查找
线性表查找属于静态查找，是将查找表视为一个线性表，将其顺序或链式存储，再进行查找，因此查找思想较为简单，效率不高。如果查找表中的数据元素有一定的规律（如按关键字有序），可以利用这些信息获得较好的查找效率。
顺序查找
即数据存储在顺序表中，然后逐项查找元素。
实现：
#define MAXNUM 100 /*查找表的容量*/
typedef int KeyType;
typedef struct{
KeyType key; /*关键字字段*/
}DataType;
typedef struct{
DataType data[MAXNUM]; /*存储空间*/
int n; /*元素个数*/
}SeqList;
int Seq_Search_1 (SeqList list, KeyType kx)
{/*数据存放在list.data[1] 至list.data[n]中，在表list中查找关键字为kx的数据元素*/
/*若找到返回该元素在查找表中的位置，否则返回0*/
int i=1;
while(i<=list.n && list.data[i].key!= kx )
i++; /* 从表头端向后查找 */
if (i>list.n)
return 0;
else
return i;
}
加监视哨后的顺序查找：
int Seq_Search_2(SeqList list, KeyType kx)
{ /*数据存放在list.data[1] 至list.data[n]中，在表list中查找关键字为kx的数据元素*/
/*若找到返回该元素在查找表中的位置，否则返回0 */
int i;
list.data[0].key=kx;
i=list.n;
while(list.data[i].key!= kx )
i--; /* 从表尾端向前查找 */
return i;
}
比较次数减少了，效率提高。
顺序表上的顺序查找的性能分析
对于n个元素的查找表，若查找的是表中第i个记录时，需进行 n-i+1 次关键字比较，即 ci=n-i+1 。
设查找每个元素的概率相等。 查找成功时，顺序查找的平均查找长度为：
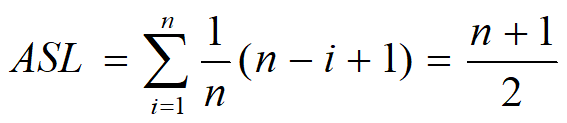
查找不成功时，表中每个关键字都要比较一次，直到监视哨，因此关键字的比较次数总是n+1次，显然时间复杂度为O(n)。
顺序查找的特点
- 顺序查找的优点是算法简单，对表中数据元素的存储方式、是否按关键字有序均无要求；
- 缺点是平均查找长度较大，效率低，当n很大时，不宜采用顺序查找。
为了提高查找效率，查找表中的数据存放需依据查找概率越高，使其比较次数越少；查找概率越低，比较次数可相对较多的原则来存储数据元素。
有序表查找
- 有序表是指查找表中的元素按关键字大小有序存储。
- 如果查找表采用顺序结构存储且按关键字有序，那么查找时可采用效率较高的折半查找算法实现。
二分查找（折半查找）
折半查找的思想为：
在有序表中，取中间元素作为比较对象，若给定值与中间元素的关键字相等，则查找成功；若给定值小于中间元素的关键字，则在中间元素的左半区继续查找；若给定值大于中间元素的关键字，则在中间元素的右半区继续查找。不断重复上述查找过程，直到查找成功，或所查找的区域无数据元素，查找失败。
算法实现：
int Binary_Search(SeqList list, KeyType kx)
{ /*数据存放在list.data[1] 至list.data[n]中，在表list中查找关键字为kx的数据元素*/
/*若找到返回该元素在表中的位置，否则返回0 */
int mid,low=1, high=list.n; /*设置初始区间 */
while(low<=high) { /*当查找区间非空*/
mid=(low+high)/2; /*取区间中点 */
if(kx==list.data[mid].key)
return mid; /* 查找成功，返回mid */
else if (kx<list.data[mid].key)
high=mid-1; /* 调整到左半区 */
else low=mid+1; /* 调整到右半区 */
}
return 0; /* 查找失败，返回0 */
}
折半查找的平均查找长度可用判定树来分析
先看一个具体的情况，假设：n=11
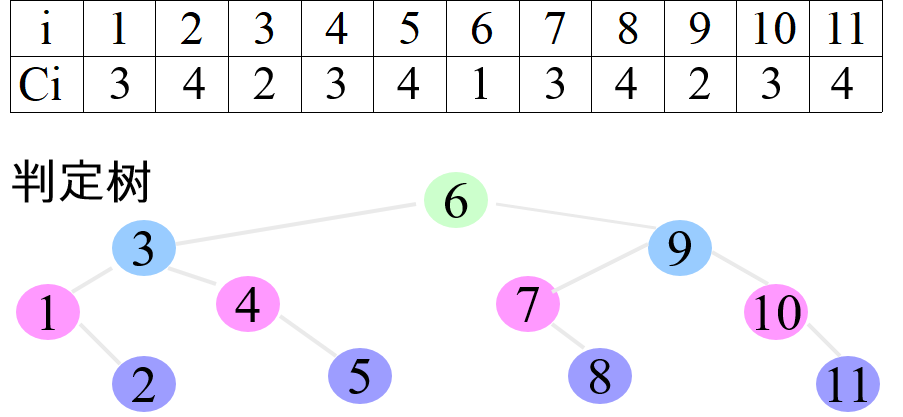
二分查找的效率（ASL）
1次比较就查找成功的元素有1个（20），即中间值；
2次比较就查找成功的元素有2个（21），即1/4处（或3/4）处；
3次比较就查找成功的元素有4个（22），即1/8处（或3/8）处…
4次比较就查找成功的元素有8个（23），即1/16处（或3/16）处…
……
则第h次比较时查找成功的元素会有（2h-1）个；
为方便起见，假设表中全部n个元素＝ 2h-1个，此时就不讨论第m次比较后还有剩余元素的情况了。
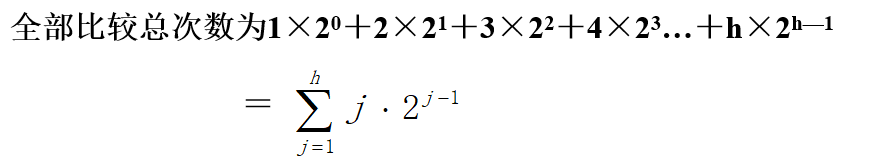
以含n个结点的满二叉树为例(n=2h-1),设查找概率相等,则二分查找的平均查找长度为：
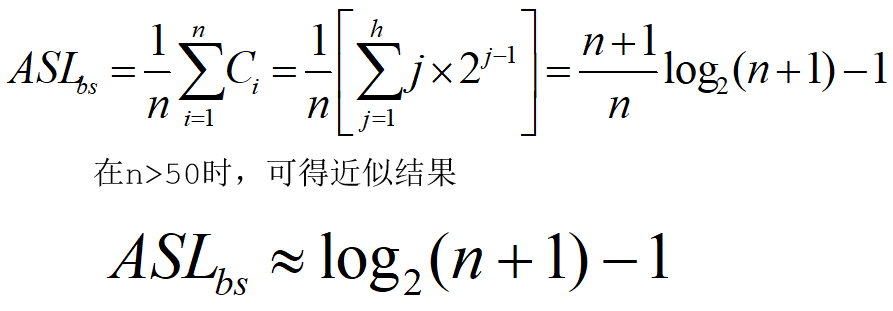
最坏情况下,关键字比较次数为log2(n+1) ，期望时间复杂度为 O(log2n)
折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再发生变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。
顺序查找与二分查找的比较
顺序查找 ：
优点：算法简单，对数据特性无要求；
缺点：ASL大，效率低。
二分查找 ：
优点：查找速度快，效率高；
缺点：需在有序表上进行，且只限于顺序存储。
插值查找
在介绍插值查找之前，首先考虑一个新问题，为什么上述算法一定要是折半，而不是折四分之一或者折更多呢？
打个比方，在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里绝对不会是从中农间开始查起，而是有一定目的的往前或往后翻。
同样的，比如要在取值范围1~10000之间100个元素从小到大均匀分布的数组中查找5，我们自然会从数组下标较小的开始查找。
经过上面的分析，折半查找这种查找方式，不是自适应的（也就是一直保持分半的）。二分查找中查找点计算如下：
mid=(low+high)/2
即
mid=low+(high−low)/2
通过类比，我们可以将查找的点改进为如下：
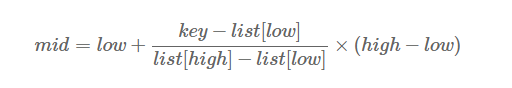
也就是将上述的比例参数1/2改进为自适应的，根据关键字在整个有序表中所处的位置，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。
基本思想： 基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，插值查找也属于有序查找。
注意： 对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。
复杂度分析： 查找成功或者失败的时间复杂度均为O(log2(log2n))。
# 插值查找算法
# 时间复杂度O(log(n))
def binary_search(lis, key):
low = 0
high = len(lis) - 1
time = 0
while low <= high:
time += 1
# 计算mid值是插值算法的核心代码
mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low]))
print("mid=%s, low=%s, high=%s" % (mid, low, high))
if key < lis[mid]:
high = mid - 1
elif key > lis[mid]:
low = mid + 1
else:
# 打印查找的次数
print("times: %s" % time)
return mid
print("times: %s" % time)
return -1
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
result = binary_search(LIST, 444)
print(result)
View Code
分块查找
分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。
索引表就是帮助分块查找的一个分块依据，其实就是一个数组，用来存储每块的最大存储值，也就是范围上限；分块就是通过索引表把数据分为几块。
基本思想：
（1）把表长为n的线性表分成m块，前m-1块记录个数为t=n/m，第m块的记录个数小于等于t；
（2）在每一块中，结点的存放不一定有序，但块与块之间必须是分块有序的；
（3）为实现分块检索，还需建立一个索引表。索引表的每个元素对应一个块，其中包括该块内最大关键字值和块中第一个记录位置的指针。
在每需要增加一个元素的时候，我们就需要首先根据索引表，知道这个数据应该在哪一块，然后直接把这个数据加到相应的块里面，而块内的元素之间本身不需要有序。因为块内无须有序，所以分块查找特别适合元素经常动态变化的情况。
分块查找只需要索引表有序，当索引表比较大的时候，可以对索引表进行二分查找，锁定块的位置，然后对块内的元素使用顺序查找。这样的总体性能虽然不会比二分查找好，却比顺序查找好很多，最重要的是不需要数列完全有序。
分块有序表的索引存储表示
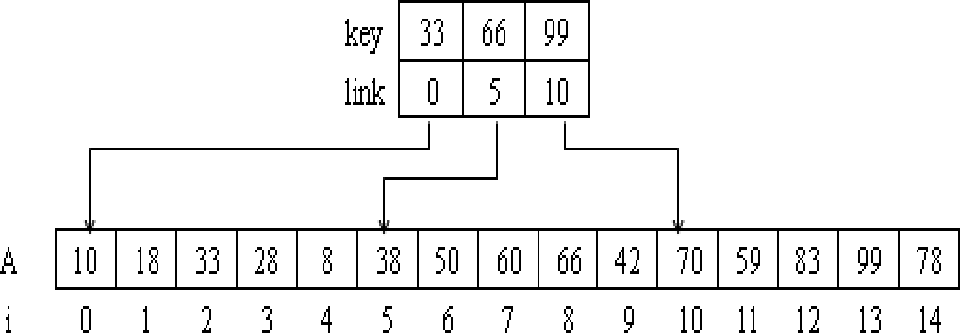
#include<stdio.h>
#define MAXL 100 //数据表的最大长度
#define MAXI 20 //索引表的最大长度
typedef int keyType;
typedef char infoType[10];
typedef struct
{
keyType key; //KeyType为关键字的数据类型
infoType data; //其他数据
}nodeType;
typedef struct
{
keyType key;
int link; //指向对应块的起始下标
}IdxType;
typedef IdxType IDX[MAXI]; //索引表类型
typedef nodeType seqList[MAXL]; //顺序表类型
int IdxSearch(IDX I, int m, seqList R, int n, keyType k)
{ // 共n个元素, m块
int low=0, high=m-1, mid, i;
int b= n/m; //b为每块的记录个数
while(low<=high) //在索引表中进行二分查找,找到的位置存放在low中
{
mid = (low+high)/2;
if(I[mid].key >= k)
high = mid-1;
else
low = mid+1;
}
//应在索引表的high+1块中,再在线性表中进行顺序查找
i = I[high+1].link; //分块中的起始下标
while(i<=I[high+1].link+b-1 && R[i].key != k) //I[high+1].link+b-1 块长度
i++;
if(i<=I[high+1].link+b-1)
return i+1;
else
return 0;
}
int main()
{
int i,n=25,m=5,j;
seqList R;
IDX I= {{14,0},{34,5},{66,10},{85,15},{100,20}};
keyType a[]= {8,14,6,9,10,22,34,18,19,31,40,38,54,66,46,71,78,68,80,85,100,94,88,96,87};
keyType x=85;
for (i=0; i<n; i++)
R[i].key=a[i];
j=IdxSearch(I,m,R,n,x);
if (j!=0)
printf("%d是第%d个数据\n",x,j);
else
printf("未找到%d\n",x);
return 0;
}
View Code
索引顺序表＝索引＋顺序表
一般情况下，索引为有序表。 分块查找步骤：
1）由索引确定记录所在区间；
2）在顺序表的某个区间内进行顺序查找。
可见，索引顺序查找的过程也是一个“缩小区间”的查找过程。
分块查找性能分析
分块查找的ASL=查找“索引”的ASL+查找“顺序表”的ASL
设n个数据元素的查找表分为m个子表，且每个子表均为t个元素，即：m*t=n
设在索引表上的检索也采用顺序查找，这样，分块查找的平均查找长度为：
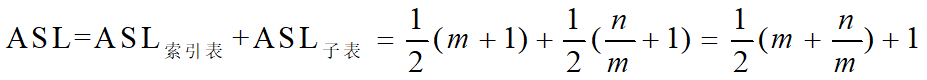
顺序表静态查找方法的比较
在上述3种查找方法中
二分查找 具有最高的查找效率，但要求必须是顺序存储结构且元素有序排列，且若要进行插入、删除运算时，因需移动大量元素，运行效率将降低，所以二分查找只适用于有序表的静态查找；
顺序查找 效率最低，但对线性表无任何要求——顺序存储或链式存储都可，是否有序都无影响；
分块查找 是顺序查找和二分查找的综合。
