>引言
在本系列第5篇《小白也能玩转数组和链表啦!》中,给出了常用数据结构的全貌图:
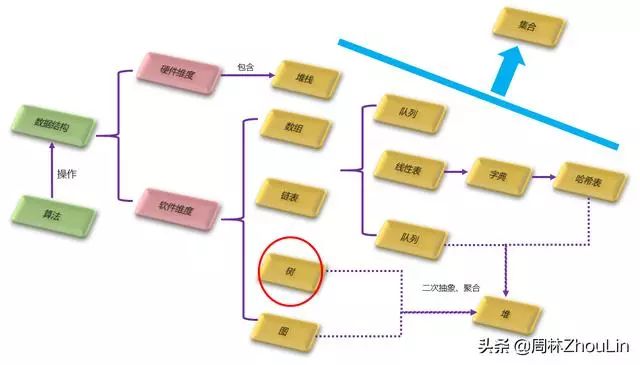

本文就来讲讲“树”这个数据结构。
1. 树的本质是什么?
本系列第2篇《扫雷还可以这样玩》中提到了算法问题的基本类型——搜索、排序、规划、计算。其中,搜索和排序与生活中朴素的体验息息相关。
我们每个人都有如下体验:
如果房间乱七八糟,那么找一样东西相当棘手。




收拾好房间之后,找东西就容易多了。收拾的过程就是分类、整理的过程。




当东西特别多时,往往一个分类还不够——这会导致该分类下的东西太多,找起来仍然很花时间。但是直接简单增加分类的话,当分类增加到一定程度,我们查找分类的时间就会变长。那么怎么解决这个矛盾呢?
方法就是给分类进行分层。每一层只有几个类,每个类再往下一层分成更细的几个类,以此类推。通过这种方法,每查找一层的时候,只用对付几个类即可。
人的大脑是通过神经元之间的连接进行思考的,神经元的排列和连接也是分层的。这样的生理结构导致我们适合做分层分类的处理。




现代科学理论也是按照这样的分层分类的方式进行组织的,源头可以追溯到古希腊的数学家欧几里得。
当年他就是用这样的分层分类的“公理化”方法,将那个时代的几何知识进行了有效组织,,写成了不朽的巨著《几何原本》,使得原本分散的海量结论,通过这样的整理,便于后人高效掌握。








这种方式,也被大名鼎鼎的物理学家恩斯特·马赫称为“智力经济”。


如果把每一个分类用一个节点来表示,位于相同层次的分类放在一行,那么整个组织结构就如下图所示:
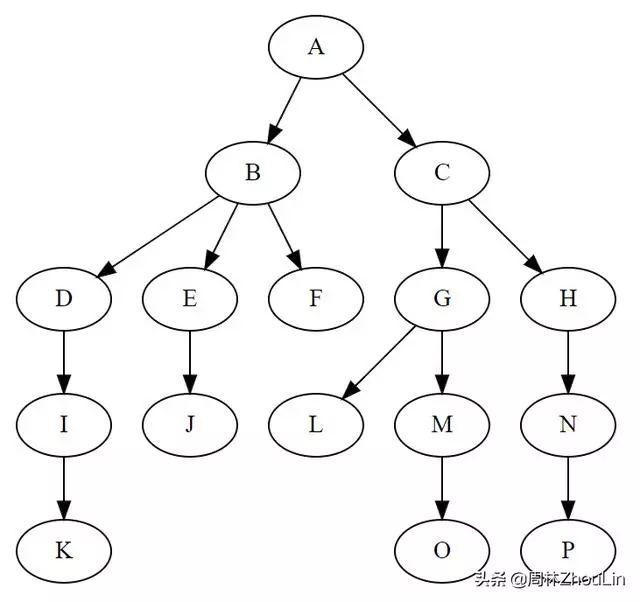

看起来是不是像一颗倒过来的树?


综上所述:树的本质就是一种用于高效搜索的数据结构。
更进一步,如果树中的节点之间还有排序关系,那么搜索还会加速。
二叉树
既然讨论分类,我们就从最简单、最常用的分类——二元分类开始研究。所谓的二元分类,用通俗的话来说就是:非黑即白。对应到树的结构,如下图所示:
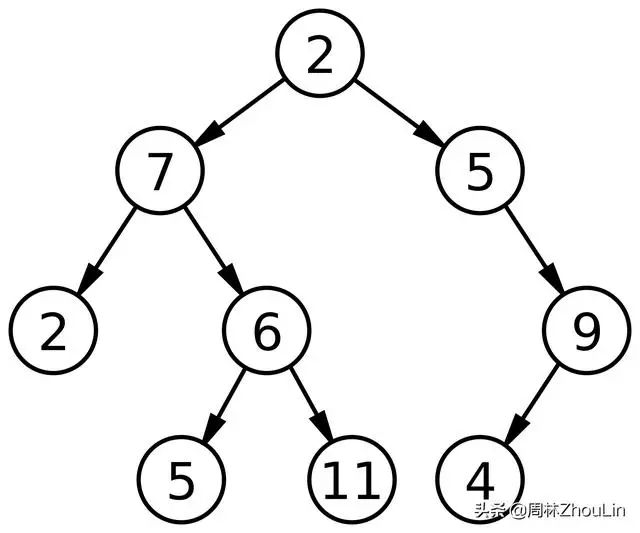

它的特点就是:每个节点最多只有两个分支(子节点)。
2. 二叉树的数据结构表达
从上图可以看出,整棵树其实就是一个递归结构。递归的基本单元就是节点。每个节点有三个信息:
节点本身承载的数据、节点的左子节点、节点的右子节点。
这三个信息在具体的编程语言中,可以用一个结构体或者类来表达。
这里以Java作为示例:
class BinaryNode<T> {
T node_item;BinaryNode<T> left_child;BinaryNode<T> right_child;
}
节点集合起来就是一棵树。
那么怎样集合起来呢?回头看看本文开头的那张数据结构全貌图,所有的数据结构都可以用作集合。本系列第5篇《小白也能玩转数组和链表啦!》中介绍的数组和链表就是常用的用来将节点组织成树的数据结构。
换言之,二叉树这个数据结构是由数组或者链表这样的基础数据结构复合而成。
2.1 二叉树的链表复合形式
节点之间通过left_child和right_child勾连起来就形成了树。
假设有一组节点Node_0、Node_1、Node_2、Node_3,Node_4,Node_5,它们之间的关系如下:
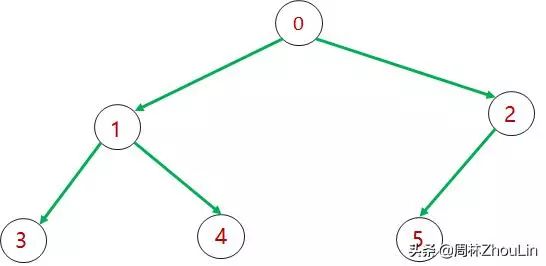

那么用链表复合就是通过如下代码:
Node_0.setLeftChild(Node_1);
Node_0.setRightChild(Node_2);
Node_1.setLeftChild(Node_3);
Node_1.setRightChild(Node_4);
Node_2.setLeftChild(Node_5);
Node_2.setRightChild(null); // 没有对应的子节点,就设置为空节点
其中setLeftChild()定义成设置左子节点的方法:
public void setLeftChild(BinaryNode<T> left) {
this.left_child = left;
}
setRightChild()定义成设置右子节点的方法。
public void setRightChild(BinaryNode<T> right) {
this.right_child = right;
}
2.2. 二叉树的数组复合形式
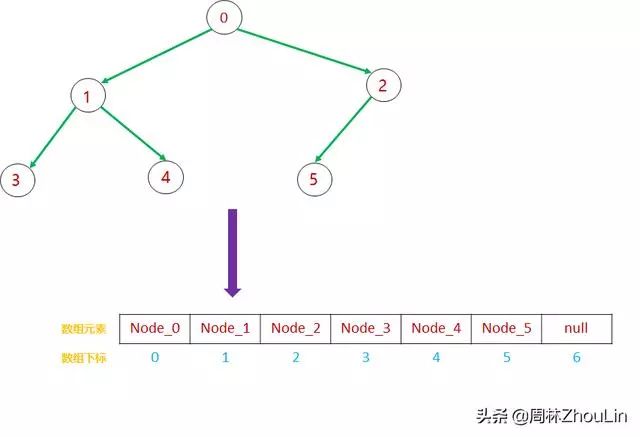
按照从上到下、从左到右的顺序,可以依次将各节点放入一个数组:
数组的第0号元素是树的根节点(node_0),第1号元素是根节点的左子节点(node_1),依此来推。

3. 完全二叉树
如果一棵二叉树,除了末尾的那些节点外,其他节点都是两个分支(子节点),那么这样的二叉树就叫作“完全二叉树”:

将完全二叉树用空节点补齐,就成为了满二叉树。
5. 为什么研究完全二叉树和满二叉树?
因为完全二叉树和满二叉树有比较好的性质,这样的性质可以被用于高效搜索、排序。
5.1 深度与节点总数的关系
先来看满二叉树。
由满二叉树的定义可知:每个节点都在下一层“裂变”成2个节点。如果当前层的节点总数为N的话,那么下一层的节点总数就是2N。假若我们记第h层的节点总数为f(h),那么:
f(1):f(2):f(3): ... :f(n)=1:2:4: ... :2^(h-1) (式1)
显然这构成一个等比数列。
整个满二叉树(假设总共h层)的节点总数M等于:
f(1)+f(2)+f(3)+...+f(h)=1+2+4+...+2^(h-1)
根据等比数列求和公式得到:
M=f(1)+f(2)+f(3)+...+f(h)=1+2+4+...+2^(h-1)=2^h-1(式2)
h其实代表树的深度,对上式两边取以2为底的对数,得到:
h=logM (式3)
如果是完全二叉树,假设:
(1)该完全二叉树的节点总数是m、深度是h;
(2)将它“补全”的满二叉树的节点总数是M、深度是H;
(3)将它“补全”的满二叉树的深度是H;
那么根据完全二叉树和满二叉树的定义可知:
H-1<h<=H(式4)M-m<=f(H) (式5)
将式3代入式4得到:
logM-1<h<=logM(式6)
将式1打入式5得到:
M-m<=2^(H-1)(式7)
5.2 节点与子节点位置的线性关系
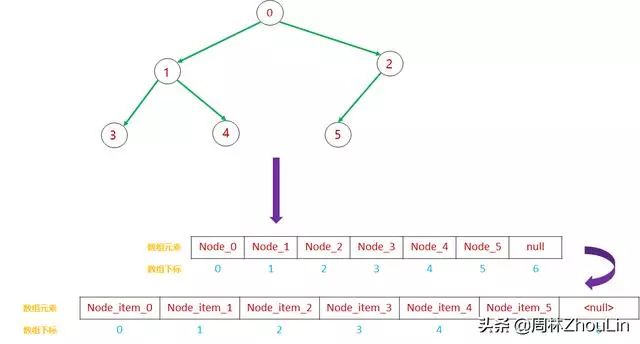
从完全二叉树的数组复合形式表达可以发现:
第0号元素所代表的节点,它的左子节点是数组的第1号元素,它的右子节点是数组的第2号元素;
第1号元素所代表的节点,它的左子节点是数组的第3号元素,它的右子节点是数组的第4号元素……
看出什么规律了吗?
1=2x0+12=2x(0+1)3=2x1+14=2x(1+1)
推论5.2.1
数组第n号元素所代表的节点,它的左子节点是数组的第(2n+1)号元素,它的右子节点是数组的第2(n+1)号元素

根据上述推论,我们发现一个重要事实:
每个节点的左子节点和右子节点在数组中的位置是可以直接由该节点在数组中的位置决定的。
既然相互之间的位置可以直接决定,那么也就没有必要在每个节点的数据结构中保存左子节点和右子节点的信息了,只用保留节点本身的信息node_item即可。
6. 完全二叉树性质的应用
还记得上一篇《史上最猛之递归屠龙奥义》中的反转二叉树的题目吗?今天我们就利用满二叉树的节点与子节点位置的线性关系来巧解这道题:
反转二叉树就是递归交换左右子树,如果将整棵树用数组来保存,那么这个递归交换就可以翻译成:
遍历整个数组,对每个元素,找到它的左子节点所对应的数组元素、右子节点所对应的数组元素,将两者交换位置,就实现了整棵树的反转。
是不是很有意思呢?
7. 下一步展望<
看到这里,相信你对树已经有了扎实的理解。接下来我们的小汽车会逐步加速,带你畅游查找二叉树、平衡二叉树、B树和红黑树等高阶“乐园”。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
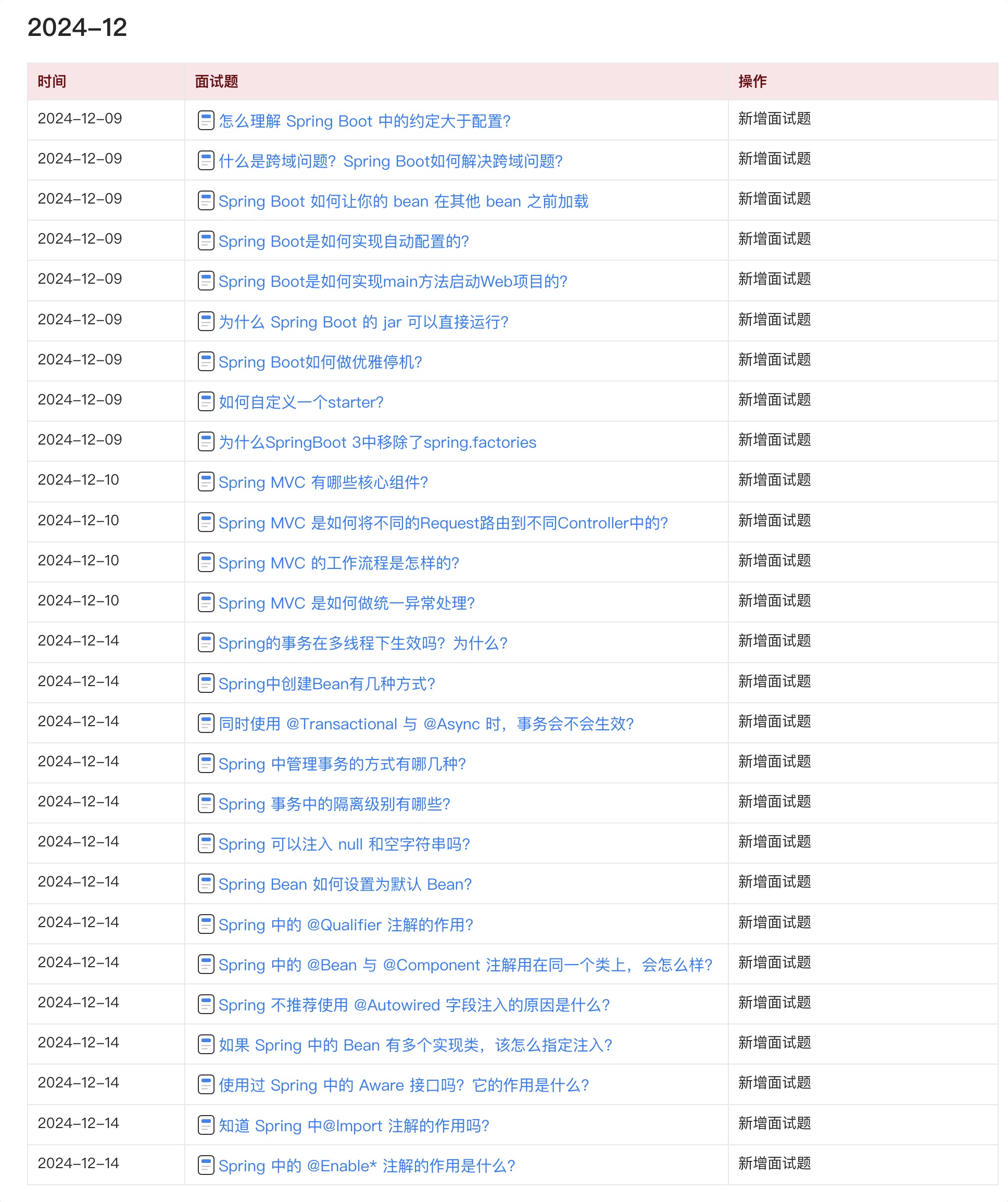
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

