数据结构与算法—二叉树的遍历

二叉树遍历的几种方法

存储结构：

    typedef char ElemType;
    typedef struct BiTNode{
      ElemType data;
      struct BiTNode *lchild,*rchild;
    }BiTNode;

遍历

树的遍历顺序是相对父结点来说的。

先序遍历：

先访问根结点,然后分别先序遍历左子树、右子树。

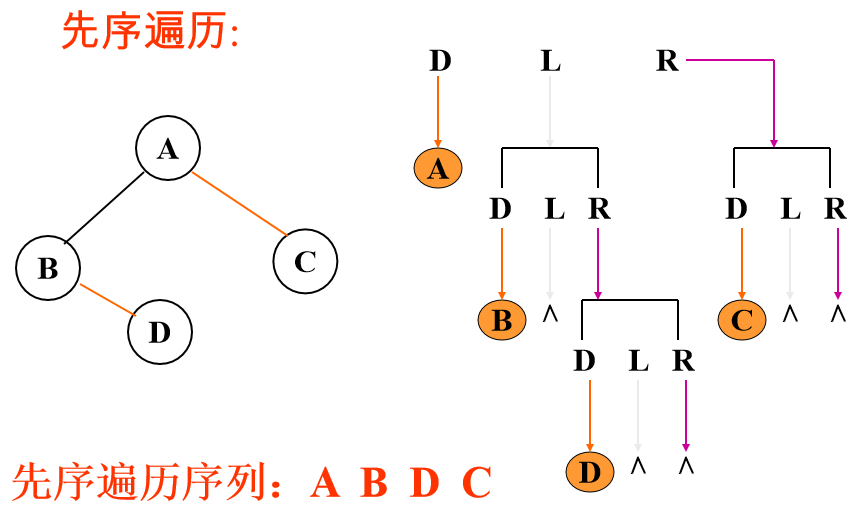
递归先序：

    void PreOrderTraverse(BiTree bt)
    { /* 最简单的Visit函数：Visit(ElemType  e){printf(e);}*/
        if(bt){
            Visit(bt->data);
            PreOrderTraverse(bt->lchild);
            PreOrderTraverse(bt->rchild);
        }
    }

非递归先序：

p=根结点地址，初始化栈
while(p!=NULL || 栈不空)

while(p!=NULL ) 访问p, p入栈, p=p->lchild

若栈不空，出栈p，p=p->rchild

    void inorder_fdg(BiTNode *bt) /*非递归先序遍历*/
    {   int top=0;
        BiTNode *p,*s[20];   p=bt;
        while(p!=NULL||top>0) {
           while(p!=NULL){   
               printf("%c ",p->data);   // 先序遍历
               s[top++]=p; p=p->lchild;
           }
           if(top>0)
           {   p=s[--top];
               //printf("%c ",p->data); // 中序遍历
               p=p->rchild;
           }
        }
    }

中序遍历 ：

先中序遍历左子树，然后访问根结点，最后中序遍历右子树。

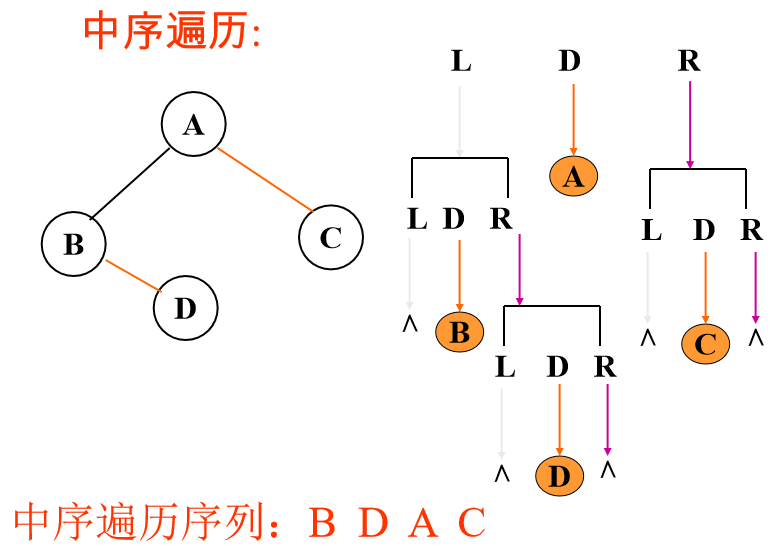
    void InOrderTraverse(BiTree bt)
    { 
        if(bt){
            PreOrderTraverse(bt->lchild);
            Visit(bt->data);
            PreOrderTraverse(bt->rchild);
        }
    }

后序遍历 ：

先后序遍历左、右子树，然后访问根结点。

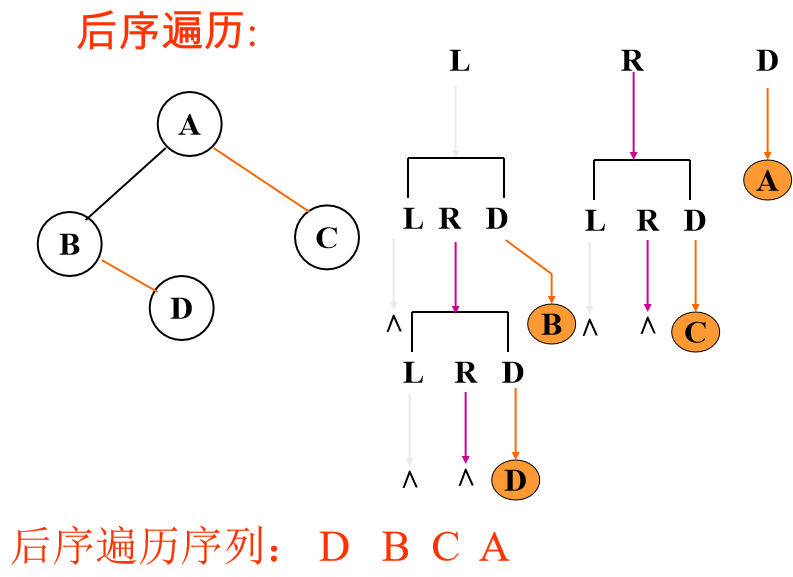
    void InOrderTraverse(BiTree bt)
    { 
        if(bt){
            PreOrderTraverse(bt->lchild);
            PreOrderTraverse(bt->rchild);
            Visit(bt->data);
        }
    }

按层次遍历 ：

从上到下、从左到右访问各结点。

可使用一个顺序存储的队列q[100],存放还没有处理的子树的根结点的地址。注意,队首和队尾指针分别指向队首结点和下次进队结点的存放位置。

首先把根节点入队。
然后访问队头的一个结点，再把该结点非空的左右子树入队。
如果队列不空，重复2)。

    void lev_traverse(BiTNode* T)
    { /* 用队列实现层次遍历 */
      BiTNode *q[100],*p;
      int head,tail;  
      q[0]=T;head=0;tail=1;
      while(head<tail) { /* 当队列不空 */
        p=q[head++];
        printf("%c ",p->data);
         if(p->lchild!=NULL)
          q[tail++]=p->lchild;
         if(p->rchild!=NULL)
          q[tail++]=p->rchild;
      }
    }

其他

先中后层的例子：

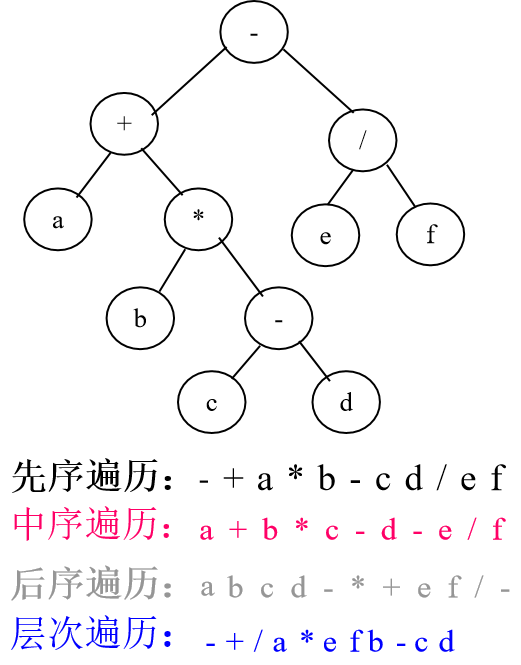
求二叉树的深度(后序遍历)

算法基本思想:

从二叉树深度的定义可知，二叉树的深度应为其左、右子树深度的最大值加1。

由此，需先分别求得左、右子树的深度，算法中“访问结点”的操作为：求得左、右子树深度的最大值，然后加 1 。

    //计算二叉树的深度
    int Depth(BiTNode *bt)
    {
        int depth, depthLeft, depthRight;
        if (bt == NULL)
            depth = 0;
        else  {
            depthLeft = Depth(bt->lchild);
            depthRight = Depth(bt->rchild);
            depth = 1 + (depthLeft > depthRight ? depthLeft : depthRight);
        }
        return depth;
    }

Java 面试宝典是大明哥全力打造的 Java 精品面试题，它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题，而是一套完整的 Java 知识体系，一套你 Java 知识点的扫盲贴。

它的内容包括：

大厂真题：Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
原创内容：Java 面试宝典内容全部都是大明哥原创，内容全面且通俗易懂，回答部分可以直接作为面试回答内容。
持续更新：一次购买，永久有效。大明哥会持续更新 3+ 年，累计更新 1000+，宝典会不断迭代更新，保证最新、最全面。
覆盖全面：本宝典累计更新 1000+，从 Java 入门到 Java 架构的高频面试题，实现 360° 全覆盖。
不止面试：内容包含面试题解析、内容详解、知识扩展，它不仅仅只是一份面试题，更是一套完整的 Java 知识体系。
宝典详情：https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
宝典总览：https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
宝典进展：https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw

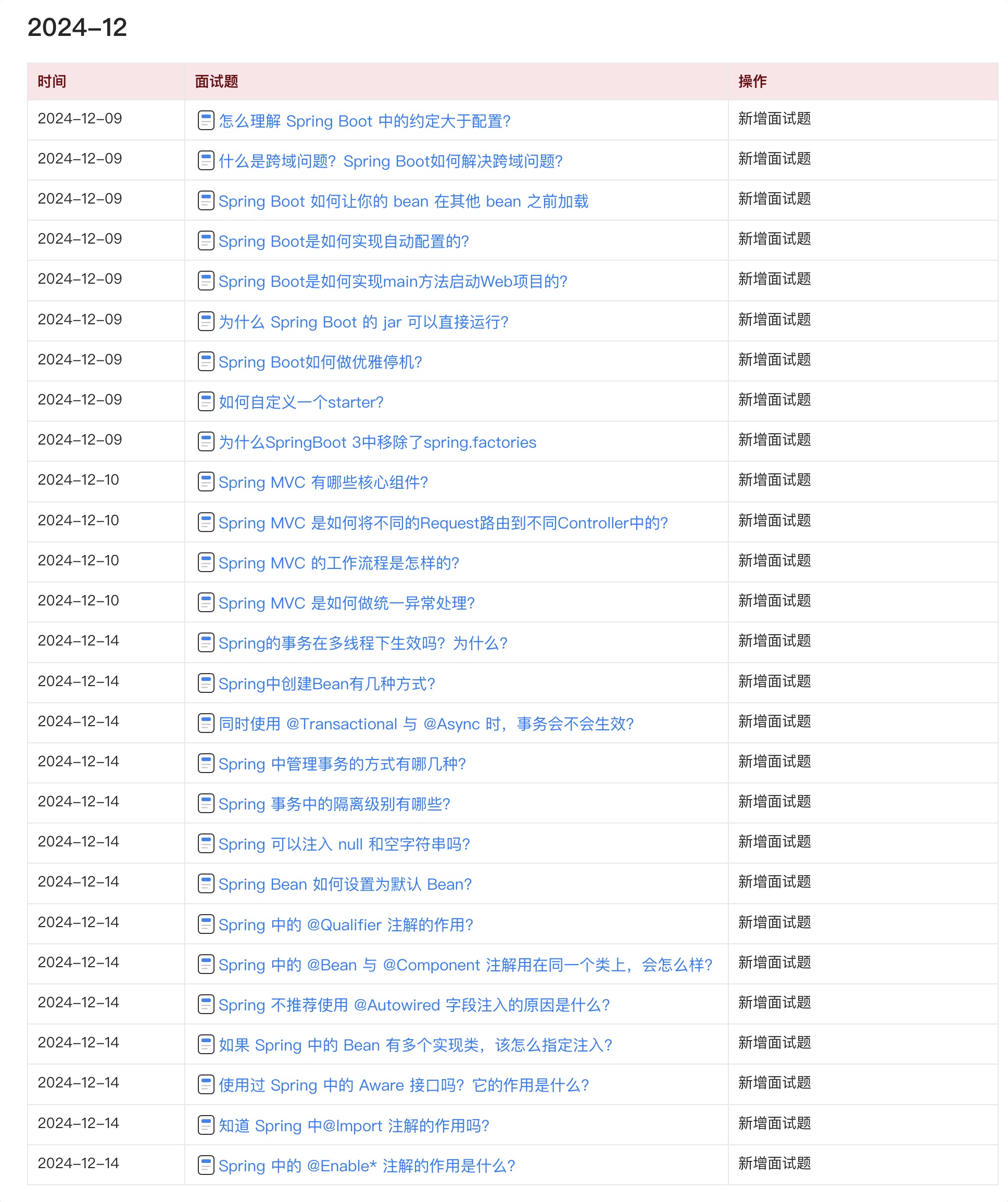
目前 Java 面试宝典累计更新 400+ 道，总字数 42w+。大明哥还在持续更新中，下图是大明哥在 2024-12 月份的更新情况：

想了解详情的小伙伴，扫描下面二维码加大明哥微信【daming091】咨询

同时，大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ，回复【面试题】即可免费领取。

阅读全文