题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------
做这道题之前一定要对前序遍历和中序遍历非常理解,刚开始由于我没有很好的理解他们,画图的时候一直卡着,差点以为是题目的例子错了,不过后来很好,看了朋友画的图反应过来了;
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------
这道题主要是你得有node的结点意识,每个点往下层又是一个root结点;以这种思想然后进行递归,问题就很好解决了;
首先对例子进行分析:
前序遍历序列{1,2,4,7,3,5,6,8}
中序遍历序列{4,7,2,1,5,3,8,6}
这里面你首先根据前序遍历可知道root结点是1,然后又根据中序遍历你可以知道1左边的都是root根结点的左孩子群{4,7,2},1右边的都是root根结点的右孩子群{5,3,8,6};
根据上面我们可以画出第一个结点:
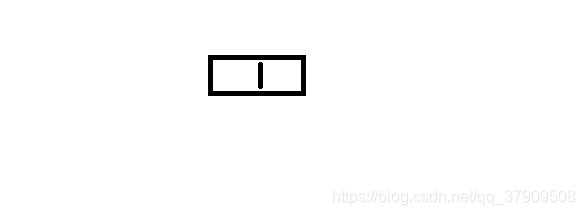
这样你可以先进入root根结点的左孩子群里面;root(1)的左孩子是2,在这里你就得把左孩子直接看成一个root根结点,其他的暂时都不用想,这样的话,以root根结点来看它的:
前序遍历序列{2,4,7}
中序遍历序列{4,7,2}
这里面你又根据前序遍历可知道root结点是2,然后根据中序遍历你可以知道2左边的都是root(2)根结点的左孩子群,2右边没有,说明没有右孩子群;
根据上面我们可以画出第二个结点:
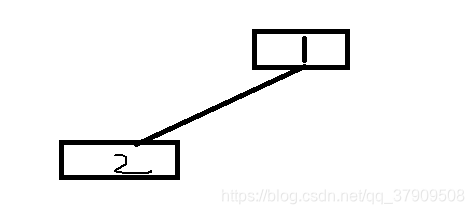
你又进入到root(2)的左孩子群里面,以4作为根结点继续:
前序遍历序列{4,7}
中序遍历序列{4,7}
以4做为root(4)结点,根据中序遍历发现它没有左孩子只有一个右孩子,那么在这里开始遍历它的右子树,得出它俩如下的位置:
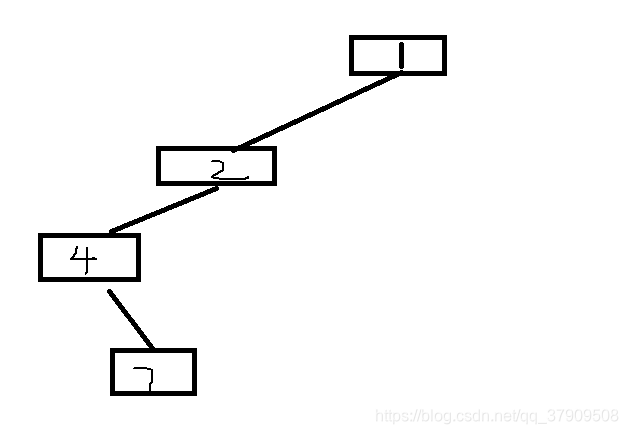
回到上一个的右子树群,一直追溯回去发现,也就只剩下是root(1)的右子树没有遍历了,然后直接又以右子树建立前序遍历和中序遍历:
前序遍历序列{3,5,6,8}
中序遍历序列{5,3,8,6}
根据前序遍历的性质,以root(3)为根结点,由中序遍历可知3左边的{5}为左孩子群,{8,6}为右孩子群;现在可以又可以确定一个结点:
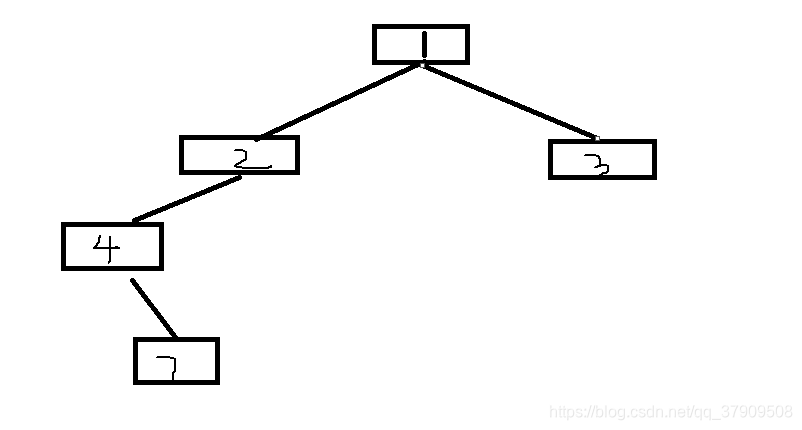
以root(3)为根简单分析它的左孩子群:
前序遍历序列{3,5}
中序遍历序列{5,3}
根据中序遍历可知5是root(3)的左孩子,root(3)没有右孩子,又可以画出一个结点:
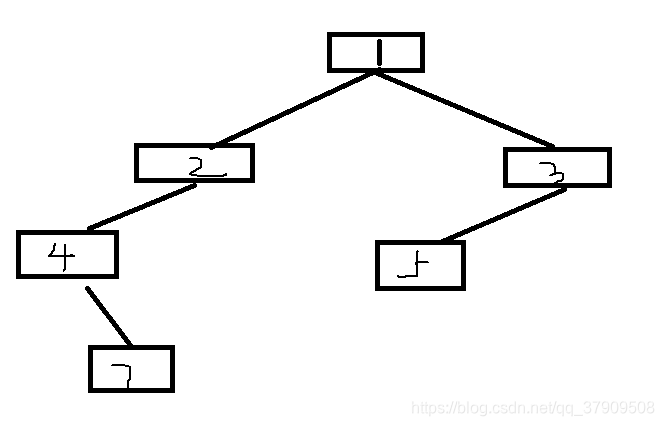
由于root(5)已经没有左孩子和右孩子了,又回到root(3)分析它的右孩子:
前序遍历序列{6,8}
中序遍历序列{8,6}
根据前序遍历root(6)为根结点,根据中序遍历root(6)左边的为左孩子群,右边的为右孩子群(很显然它没有右孩子群)
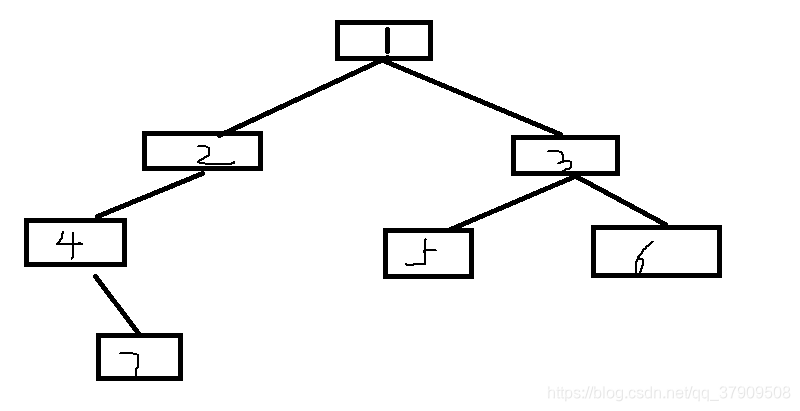
进入root(6)的左孩子群,直接得出左孩子结点为8,画出最终图像:
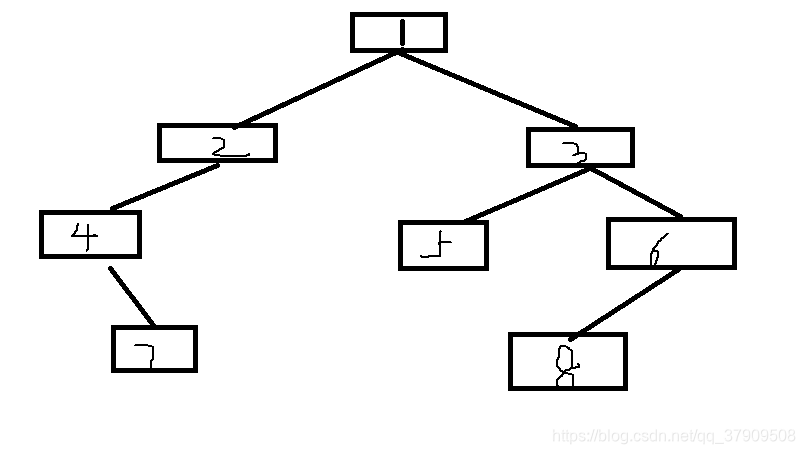
下面贴出代码:
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.*;
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
if(pre.length==0||in.length==0) {
return null;
}
TreeNode node=new TreeNode(pre[0]);
if(pre.length==1||in.length==1) {
return node;
}
for(int i=0;i<pre.length;i++) {
if(pre[0]==in[i]) {
node.left=reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i+1),Arrays.copyOfRange(in, 0, i));
node.right=reConstructBinaryTree(Arrays.copyOfRange(pre, i+1, pre.length),Arrays.copyOfRange(in, i+1, in.length));
}
}
return node;
}
}
理解上面解题的思维,程序其实并不难,只是几行代码加上两个递归;对于二叉树一定要以结点的思想去思考,这样会更容易理解.
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

