上一篇博客我们讲解了信息的在计算机中是如何存储以及如何表示的。但是对于各个进制的转换 LZ 只是一笔带过了,后来LZ仔细研究了进制转换的原理,发现还是挺有感悟的。那么这篇博客就讲讲进制转换。
1、进制的介绍
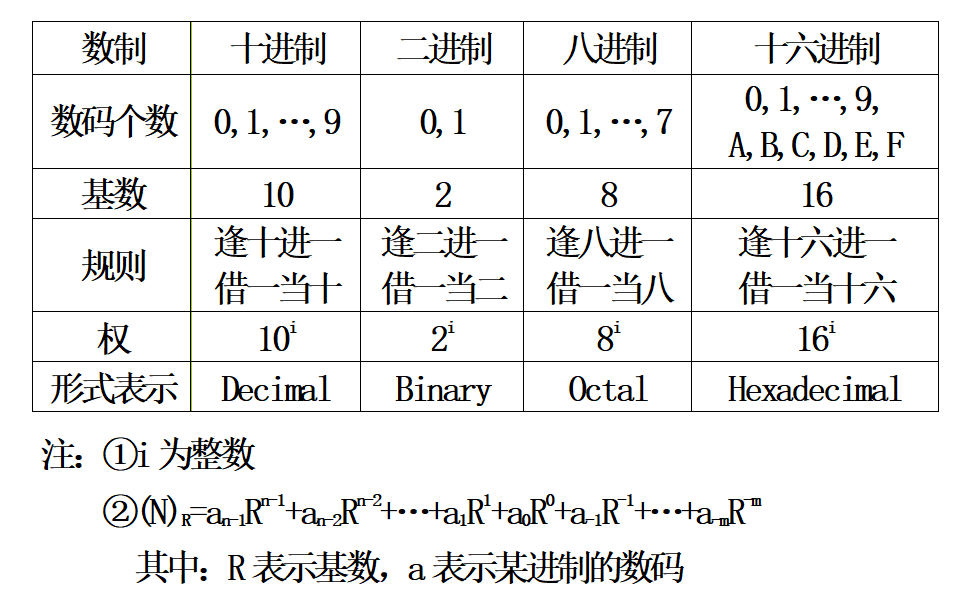
在讲进制之前,我们先看一下数制的定义: 用一组固定的数字和一套统一的规则来表示数目的方法称为数制。
** ** 而数制有进位计数制与非进位计数制之分。非进位计数制的数码表示的数值大小与它在数中的位置无关,这里我们不作过多的介绍。
进位计数制的数码所表示的数值大小则与它在数中所处的位置有关,常见的有二进制、十进制、十六进制,我们这里也只介绍这三种进制的转换。
进位计数制的要素:
①、数码:用来表示进制数的元素。比如二进制数的数码为:0,1。十进制数的数码为:0,1,2,3,4,5,6,7,8,9。十六进制数的数码为:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
②、基数:数码的个数。比如二进制数的基数为2。十进制数的基数为10。十六进制数的基数为 16.
③、位权:数制中每一固定位置对应的单位值称为位权。例如十进制第2位的位权为10,第3位的位权为100;而二进制第2位的位权为2,第3位的位权为4,对于 N进制数,整数部分第 i位的位权为N^(i-1),而小数部分第j位的位权为N^-j。
那么我们可以说: 每个数码所表示的数值=该数码值 * 所处位置的位权。 上面的内容概括起来可以看一下下面这张图:
比如十进制数:(123.45)10=1×102+2×101+3×100+4×10-1+5×10-2
** ** 二进制数:(1010)2 =l× 23+0 × 22+l× 21+0 × 20=(10)10
十六进制数:(BAD)16 =11× 162+10×161+13×160=(2989)10
2、二进制转换成其他进制
①、二进制(Binary)——>十进制(Decimal)
诀窍:以小数点为界,整数位从最后一 位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则 从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
例子:将二进制数(10.10101)2转化为十进制数。
(10.10101)2=(1x21+0x20+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(2+0+0.5+0+0.125+0+0.03125)10=(2.65625)10
②、二进制(Binary)——>十六进制(Hex)
诀窍: 因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
例子:将二进制数(10.10101)2转化为十六进制数。
(10.10101)2=(0010.1010 1000)2=(2.A8)16
3、十进制转换成其他进制
①、十进制(Decimal)——>二进制(Binary)
** ** 诀窍: 以小数点为界,整数部分除以2,然后取每次得到的商和余数,用商继续和2相除,直到商小于2。然后把第一次得到的余数作为二进制的个位,第二次得到的余数作为二进制的十位,依次类推,最后一次得到的小于2的商作为二进制的最高位,这样由商+余数组成的数字就是转换后二进制的值(整数部分用除2取余法);小数部分则先乘2,然后获得运算结果的整数部分,将结果中的小数部分再次乘2,直到小数部分为零。然后把第一次得到的整数部分作为二进制小数的最高位,后续的整数部分依次作为低位,这样由各整数部分组成的数字就是转化后二进制小数的值(小数部分用乘2取整法)。
需要说明的是,有些十进制小数无法准确的用二进制进行表达,所以转换时符合一定的精度即可,这也是为什么计算机的浮点数运算不准确的原因。
例子1:将十进制数(93)10转换成二进制数。
93/2=46………. 1
46/2=23………. 0
23/2=11………. 1
11/2=5………… 1
5/2=2…………... 1
2/2= 1 …………… 0
(93)10=(1011101)2
例子2:将十进制数(0.3125)10转换成二进制数。
0.3125x2 = 0 . 625
0.625x2 = 1 .25
0.25x2 = 0 .5
0.5x2 = 1 .0
(0.3125)10=(0.0101)2
②、十进制(Decimal)——>十六进制(Hex)
** 诀窍:** 方法同十进制转化成二进制类似。 以小数点为界,整数部分除以16,然后取每次得到的商和余数,用商继续和16相除,直到商小于16。然后把第一次得到的余数作为十六进制的个位,第二次得到的余数作为十六进制的十位,依次类推,最后一次得到的小于16的商作为十六进制的最高位,这样由商+余数组成的数字就是转换后十六进制的值(整数部分用除16取余法); 小数部分则先乘16,然后获得运算结果的整数部分,将结果中的小数部分再次乘16,直到小数部分为零。然后把第一次得到的整数部分作为十六进制小数的最高位,后续的整数部分依次作为低位,这样由各整数部分组成的数字就是转化后十六进制小数的值(小数部分用乘16取整法)。
例子1:将十进制数(93)10转换成十六进制数。
93/16= 5………… 13 ( D )
(93)10=(5D)16
例子2: 将十进制数(0.3125)10转换成十六进制数。
0.3125x16 = 5 .0
(0.3125)10=(0.5)16
4、十六进制转换成其他进制
①、十六进制(Hex)——>二进制(Binary)
诀窍: 十六进制转换成二进制与二进制转换成十六进制相反。每一位十六进制数对应四位二进制数
例子1:将十六进制数(A7)16转换成二进制数。
(A7)16=(A 7)16=(1010 0111)2=(10100111)2
例子2:将十六进制数(0.D4)16转换成二进制数。
(0.D4)16=(0. D 4)16=(0. 1101 0100)2=(0.110101)2
②、十六进制(Hex)——>十进制(Decimal)
诀窍: 方法同二进制转换成十进制类似。 以 小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0-9,A-F)乘以16的n-1次方,然后相 加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0-9,A-F)乘以16的-n次方,然后相 加即可得到小数位的十进制数(按权相加法)。
例子1:将十六进制数(A7)16转换成十进制数。
(A7)16=(10x161+7x160)10=(160+7)10=(167)10
例子2:将十六进制数(0.D4)16转换成十进制数。
(0.D4)16=(0+13x16-1+4x16-2)10=(0+0.8125+0.015625)10=(0.828125)10
5、总结
①. 其他进制转十进制:将二进制数、十六进制数的各位数字分别乘以各自基数的(N-1)次方,其相加之和便是相应的十进制数,这是 按权相加法 。
②. 十进制转其他进制:整数部分用 除基取余法 ,小数部分用 乘基取整法 ,然后将整数与小数部分拼接成一个数作为转换的最后结果。
③. 二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,不足四位的用0补足。
④. 十六进制转二进制:每一位十六进制对应每四位二进制,不足用0补足。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
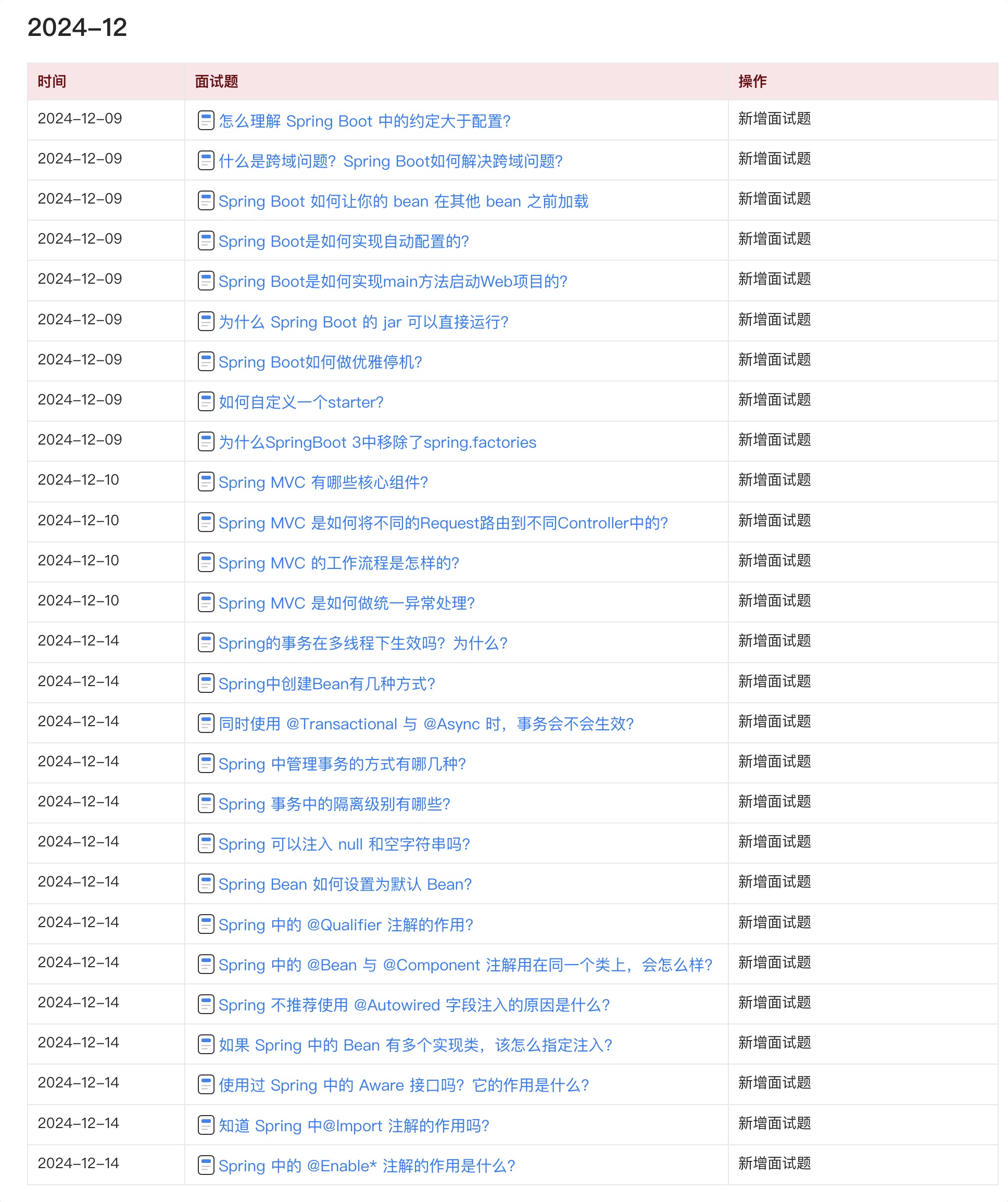
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

