上一篇博客我们讲解了二进制小数如何表示以及IEEE浮点标准。而且我们也提到过因为这种表示方法限制了浮点数的范围和精度,浮点数只能近似的表示一个数。
比如 数字1/5,我们能用十进制小数 0.2 准确的表示,但是我们却不能把它准确的表示为一个二进制小数,我们只能通过增加二进制表示的长度来提高表示的精度。如下:
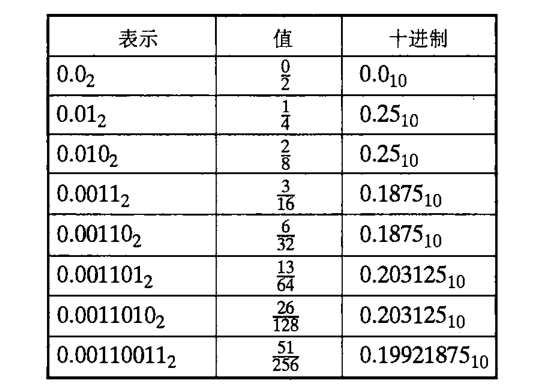
那我们该怎么办呢?
1、舍入
对于不能精确的表示的数,我们采取一种系统的方法,找到“最接近”的匹配值,它可以用期望的浮点形式表现出来,这就是舍入。
舍入一共有四种方式,分别是向偶数舍入、向零舍入、向上舍入以及向下舍入 。
可以看下面的例子:

向偶数舍入,是将数字向上或向下舍入,使得结果的最低有效数字是偶数;而向零舍入则是向靠近零的值舍入;向上舍入则是向比它大的方向靠近;向下舍入则是向比它小的方向靠近。
这四个我们可以用一个直角坐标系来理解:
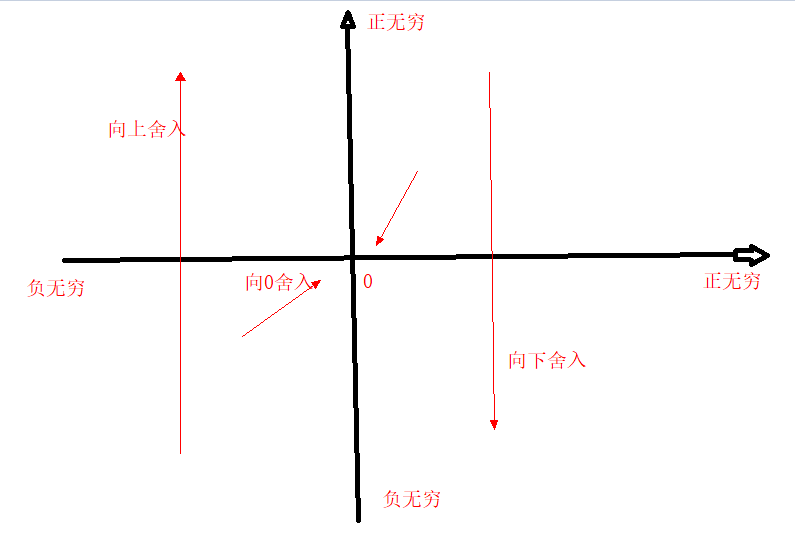
除了向偶数舍入以外,其它三种方式都会有明确的边界。这里的含义是指这三种方式舍入后的值x'与舍入之前的值x会有一个明确的大小关系,比如对于向上舍入来说,则一定有x <= x'。对于向零舍入来说,则一定有|x| >= |x'|。
那么我们什么时候会使用向偶数舍入呢?
1、比如舍入一组数值,计算这些值的平均数中引入统计偏差,如果向上舍入,那么得到的平均值会比这些数本身的平均值略高;向下舍入,则会偏低。而向偶数舍入则会避免这种偏差,在50%的时间内,它向上舍入,剩下50%的时间内,它向下舍入。
2、在我们不想舍入到整数时,我们只是简单的考虑最低有效数字是奇数还是偶数。
通常情况下我们采取的舍入规则是在原来的值是舍入值的中间值时,采取向偶数舍入,在二进制中,偶数我们认为是末尾为0的数。而倘若不是这种情况的话,则一般会有选择性的使用向上和向下舍入,但总是会向最接近的值舍入。其实这正是IEEE采取的默认的舍入方式,因为这种舍入方式总是企图向最近的值的舍入。
2、浮点运算
在IEEE标准中,制定了关于浮点数的运算规则,就是我们将把两个浮点数运算后的精确结果的舍入值,作为我们最终的运算结果。正是因为有了这一个特殊点,就会造成浮点数当中,很多运算不满足我们平时熟知的一些运算特性。
我们可以先看下面这段程序输出结果:
public void testFloat(){
float f1 = 3.14f + 10000000000f - 10000000000f;
float f2 = 3.14f + (10000000000f - 10000000000f);
System.out.println(f1);
System.out.println(f2);
}
结果都是 3.14 吗?
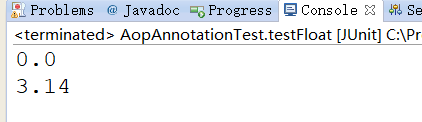
我们看到 f1 的值是0,f2的值才是3.14。为什么呢?这是因为前面3.14f+10000000000f 时,会将 3.14 这个有效数值舍入掉,而导致最终结果为0.0
f2 由于括号的存在,会先进行括号里面的运算,结果是0,然后在与3.14相加。
也就是浮点运算不满足加法的结合律 a + b + c != a + (b + c)。同时乘法结合律也不满足:a * b * c != a * (b * c);还要分配律也不满足: a * (b + c) != a * b + a * c
浮点数失去了很多运算方面的特性,因此也导致很多优化手段无法进行,比如我们试图优化下面这样一段程序。
/* 优化前 */
float x = a + b + c;
float y = b + c + d;
/* 编译器试图省去一个浮点加法 */
float t = b + c;
float x = a + t;
float y = t + d;
上面优化前是进行了四次浮点运算,而编译器优化后只需要进行三次浮点运算。但是这中间的 x 可能回产生与原始值不同的值,因为它使用了加法运算不同的结合方式。所以现在的编译器都倾向于保守的方式,避免任何对功能产生的优化,即使是很轻微的影响。
另外,浮点加法满足单调性属性:如果 a>=b,那么对于任何a、b以及 x 的值,除了 NaN,都有 x+a >= x+b。无符号或者补码加法不具有这个实数(和整数)加法的属性。
3、总结
好了,那么到此《深入理解计算机系统》前面两章的内容我们就结束了,这里我们主要需要了解无符号和补码编码格式,以及它们的运算。然后扩展到整数的表示和运算,实数的表示和运算,在实际编程中,我们会经常和数打交道,如何避免一些错误,相信看完后会有个大概的了解了。那么接下来我们将学习第三章,这将是一个全新的世界——汇编语言。这肯定比我们前面讲的要有趣多了,前面都是和0或者1这样的数字打交道,后面至少是一种编程语言,相信会更加有趣。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
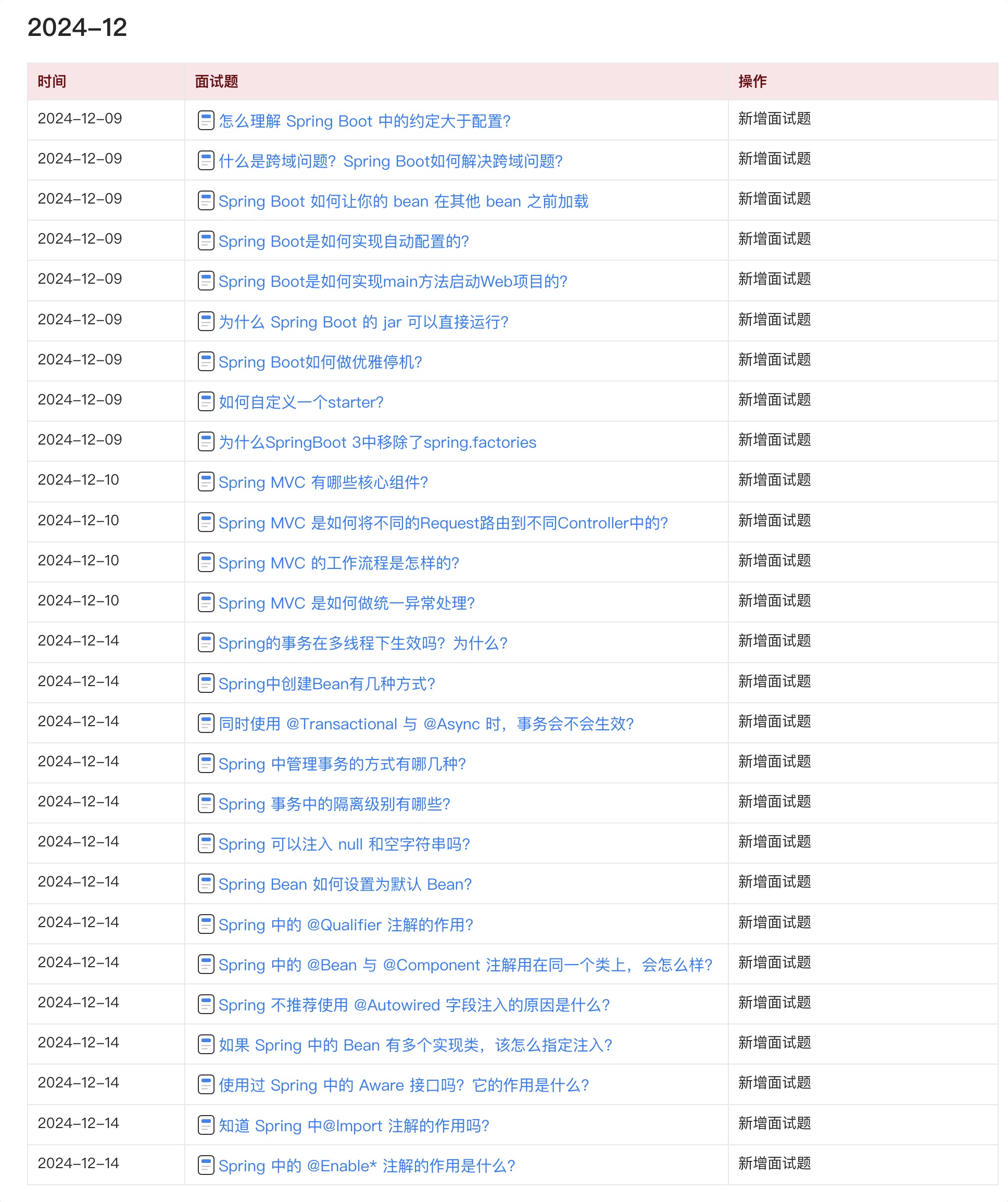
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

