我在《共识问题》一章中提到过,共识算法一共可以分为两大类:拜占庭容错算法(Byzantine Fault Tolerance,BFT)和故障容错算法(Crash Fault Tolerance,CFT)。
Leslie Lamport在论文中提出的 口信消息解决方案 就属于BFT,需要考虑恶意节点的篡改、攻击等问题。但是,口信消息解决方案在现实场景中很难落地。比如,它并不关心这个共识的结果是什么,这会出现一种情况:现在适合进攻,但将军们达成的共识却是撤退。
另外,实际场景中,我们往往需要就提议的一系列值(而不是单值)在拜占庭错误发生的时候,也能被达成共识。那应该怎么做呢?一种方案就是本文要讲解的PBFT算法。 PBFT算法,是一种能在实际场景中落地的BFT算法,它在区块链中应用广泛。
一、 oral message的问题
要理解PBFT算法,首先必须要明白 口信消息解决方案(A solution with oral message)到底存在哪些问题 ?这些问题都是后续众多BFT算法在努力改进和解决的,理解了这些问题,能帮助你更好地理解后来的拜占庭容错算法的思想(包括 PBFT 算法)。
oral message方案存在一个致命的缺陷:当将军总数为n,叛将数为f时,算法需要递归协商 f+1 轮,消息复杂度为 O(n ^ (f + 1)),消息数量指数级暴增。
你可以想象一下,如果叛将数为 64,消息数已经远远超过 int64 所能表示的了,这是无法想象的。
二、PBFT算法流程
PBFT 算法,通过签名(或消息认证码 MAC)约束恶意节点的行为,每个节点都可以通过验证消息签名确认消息的发送来源,一个节点无法伪造另外一个节点的消息。
PBFT 算法采用了 三阶段协议 ,基于大多数原则(2f + 1,f表示叛将数)实现共识。另外,与oral message不同的是,PBFT 算法实现的是一系列值的共识,而不是单值的共识。
我们先来看看PBFT 算法的流程。为了方便演示,假设一共有A、B、C、D四个节点,那么根据Paxos算法的理论,最多允许存在一个恶意节点((4-1)/3=1),我们假设B是恶意节点,现在客户端发起了一个提议值(进攻),希望被各节点达成共识:
在PBFT算法中,第一个接收到客户端请求的节点,将成为Leader节点,我们假设A节点首先接收了到请求。A接收到客户端请求之后,会执行三阶段协议(Three-phase protocol)。
2.1 预准备阶段
首先,A进入 预准备(Pre-prepare)阶段 ,构造包含作战指令的预准备消息,并广播给其他节点(B、C、D):
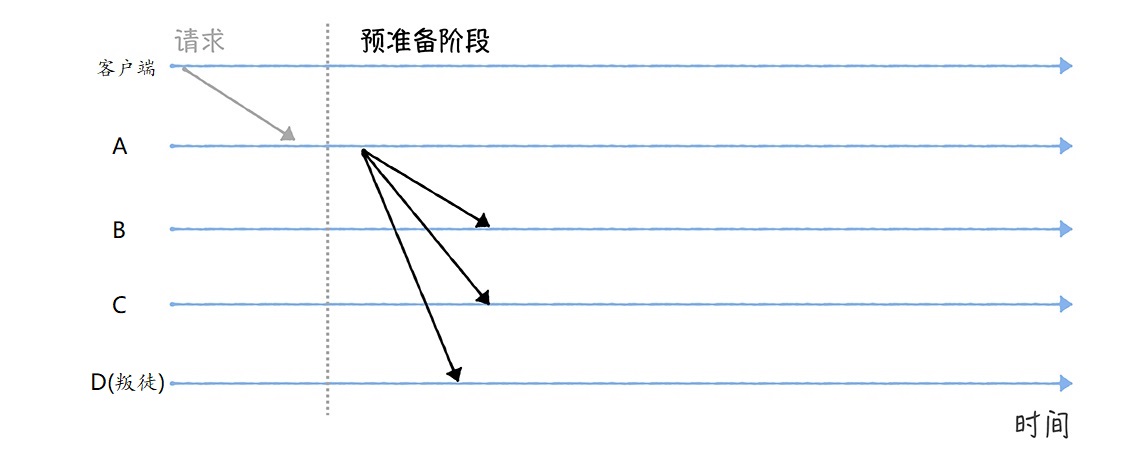
2.2 准备阶段
B、C、D收到消息后 , 不能确认自己接收到指令和其他人的是否相同。比如,D是叛徒,D收到了 2 个指令,然后他给A发送的是其中一个指令,给B、C发送的是另一个指令,这样就会出现无法一致行动的情况。
所以, 接收到预准备消息之后,B、C、D会进入准备(Prepare)阶段,并分别广播包含指令的准备消息给其他节点。这里我们假设叛徒D想通过不发送消息,来干扰共识协商:
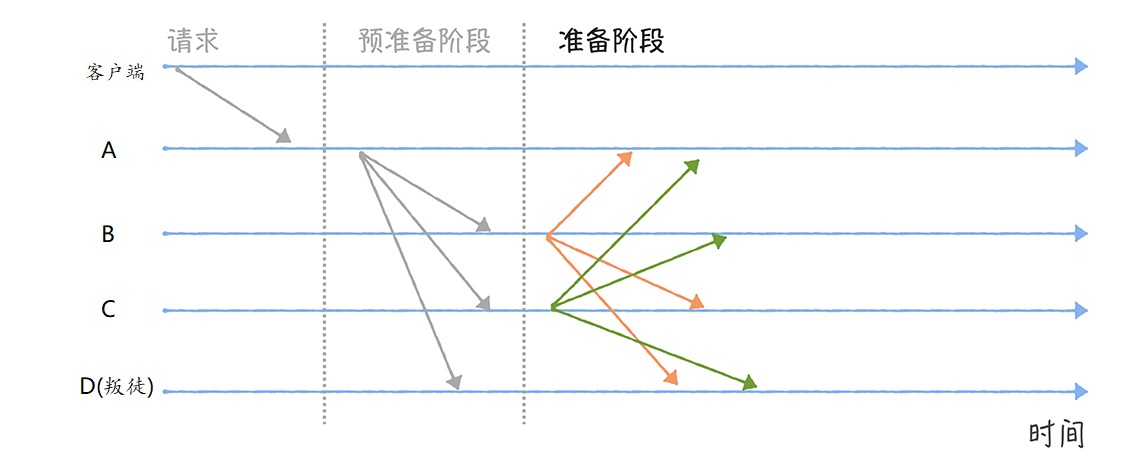
2.3 提交阶段
然后,当某个节点收到 2f 个包含相同指令的准备消息后,会进入 提交(Commit)阶段 (这里的f 为叛徒数, 2f 包括自己)。
在这里,思考一个问题:这个时候节点(比如B)可以直接执行指令吗?答案还是不能,因为B不能确认A、C、D是否收到了 2f 个一致的包含相同指令的准备消息。也就是说,B这时无法确认A、C、D是否准备好了执行指令。
进入提交阶段后,各节点分别广播提交消息给其他节点,也就是告诉其他节点:“我已经准备好了,可以执行指令了”:
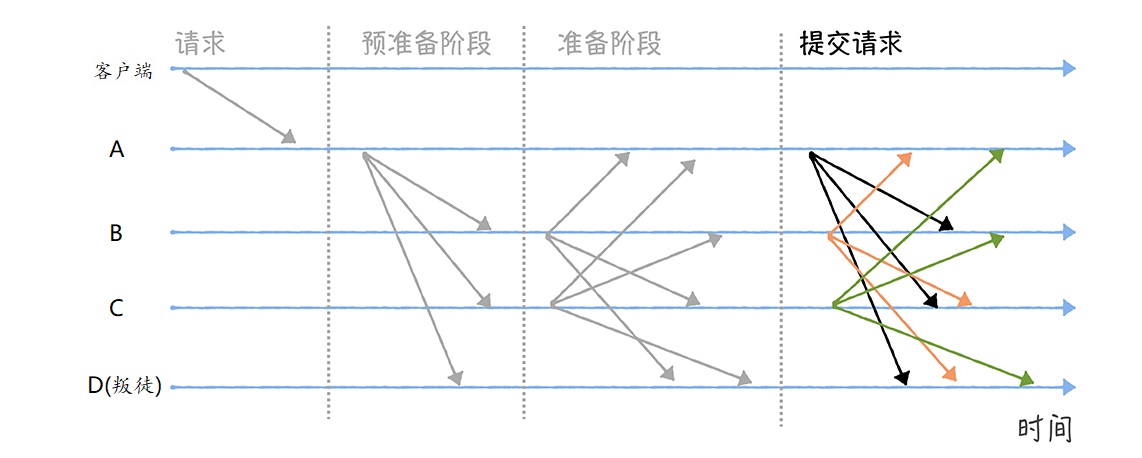
2.4 响应
最后,当某个节点收到 2f + 1 个验证通过的提交消息后(其中 f 为叛徒数,包括自己),也就是说,大部分的节点们已经达成共识,这时可以执行指令了,那么该节点将执行客户端的指令,执行完毕后发送执行成功的消息给客户端。
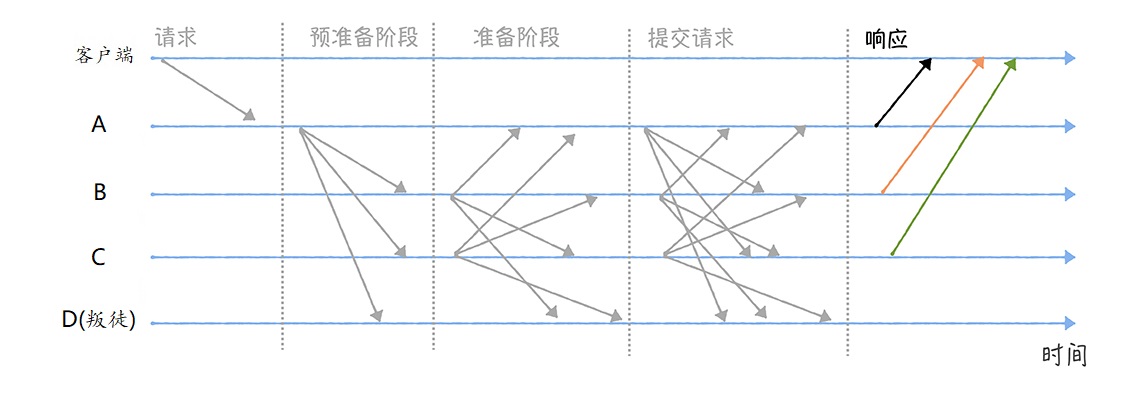
最后,当客户端收到 f+1 个相同的响应(Reply)消息时,说明各个节点已经就指令达成了共识,并执行了指令。
在PBFT算法中,共识是否达成,客户端是会做判断的,如果客户端在指定时间内未收到请求对应的 f + 1 相同响应,就认为集群出故障了,共识未达成,客户端会重新发送请求。PBFT 算法通过视图变更(View Change)的方式,来处理主节点作恶,当发现主节点在作恶时,会以“轮流上岗”方式,推举新的主节点。
三、总结
Raft 算法完全不适应有人作恶的场景,但PBFT 算法能容忍 (n - 1)/3 个恶意节点 (也可以是故障节点)。另外,相比 PoW 算法,PBFT 的优点是不消耗算力,所以在日常实践中,PBFT 比较适用于相对“可信”的场景中,比如联盟链。
此外,虽然PBFT 算法相比口信消息方案已经有了很大的优化,将消息复杂度从 O(n ^ (f + 1)) 降低为 O(n ^ 2),能在实际场景中落地并解决共识问题,但 PBFT 还是需要比较多的消息,比如在 13 节点集群中(f 为 4),一次共识协商需要 237 个消息,所以决定了 PBFT 算法适用于中小型分布式系统。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

