引言

在上篇文章《再不会"降维打击"你就Out了!》中，提到了递归算法的两个局限性。本文给出解决方案——动态编程。如果说"递归算法"是圣剑的话，那么"动态编程"就是圣衣。两者加持，你便可以爆发究极小宇宙：）

递归算法局限性详细分析

局限性1（适用性问题）：

如果“降维”前的状态集合并不方便用“降维”后的状态集合表示，即状态转移函数不好求，那么该场景使用递归不一定恰当。

下面举个例子来说明：

有两个集合A和B，A中有n个元素，B中也有n个相同元素，将A中的元素通过映射f，映射到B中的元素，映射f满足：f(f(x))=f(x)，求这样的不同映射有多少种。

根据在《再不会"降维打击"你就Out了!》中讲到的递归应用的优化套路，很容易看出，规模因子就是n，关键要求的就是状态转移函数g：f(n-1)->f(n)。

f(n-1)表示A和B各有n-1个元素时，不同映射的种数；

f(n)表示A和B各有n个元素时，不同映射的种数。

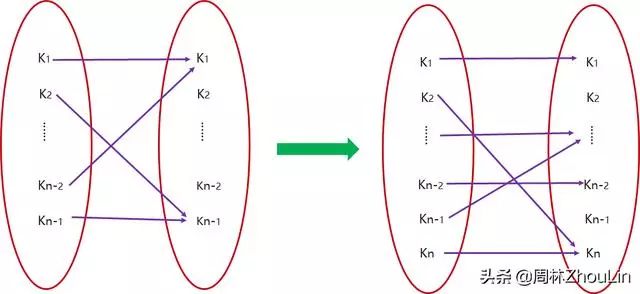
上图左侧表示的就是f(n-1)对应的一种情况，右侧表示的就是f(n)对应的一种情况。

在上面图示的情况中：

元素个数等于n-1时，A中的元素K2映射到B中的元素Kn-1；

但是元素个数等于n时，A中的元素K2映射到B中的元素Kn，此时映射的种数等价于下图映射的种数：

这是一个n-2个元素到n-1个元素的映射，显然它的值不一定等于f(n-1)。

换言之，在本例中，f(n)并不方便用f(n-1)来表示，即状态转移函数g：f(n-1)->f(n)不好求。

原因就是：

问题规模变化时，“形状”变了——从(n-1)->(n-1)变成了(n-2)->(n-1)——直观地说，从“正方形”变成了“梯形”。

如果仍然要用递归来解，那么就需要引入中间态辅助函数，计算“梯形”的函数值。

局限性2（重复计算问题）：

在直接递归的过程中部分函数值会被重复计算

为了避免重复计算，一个直接而朴素的想法就是：引入中间态辅助函数，将算过的函数值存下来，递归时再次遇到该函数时，直接从保存结果中取出来。

从上面对两个局限性的分析可以看出：优化递归的方法就是引入中间态辅助函数，保存中间态结果。

这种方法就叫做“动态编程”。

自顶向下 vs. 自底向上

很明显，保存中间态结果，有两种方式——自顶向下或者自底向上。

还是拿《再不会"降维打击"你就Out了!》中的爬台阶的例子来讲。

最终的状态转移函数表达式如下：

当n>=4时：

f(n)=f(n-1)+f(n-2)+f(n-3）

当1<=n<4时：f(n)=n

当n<1时：f(n)=0

递归的自然方向就是自顶向下。递归的同时，首先查一下保存函数值的线性表，如果查得到，那么就直接“拿来主义”；

如果查不到，那么计算完了函数值之后，也往线性表里保存结果，这样后面的递归步骤如果用得上的话，就节省计算时间了。

这里的线性表是不是有点像“备忘录”呢？所以这个方法也称作“备忘录法”

下面再来看看自底向上。我们逆着递归自然展开的方向，根据状态转移函数，一边查表一边从底部向上逐步计算函数值，并将新计算出来的值也保存到线性表中，供更高层的函数值计算时使用。这种方法就叫做“动态规划”。

由于“动态规划”是逆着递归自然展开的方向，所以写出开的程序结构不再是递归形式，而是递归展开的反向形式——循环结构。

进一步优化

细心的同学肯定发现了：无论是“备忘录法”还是“动态规划”，都要保存所有的中间结果，根据在《空间复杂度你真的懂了吗?》中学到的知识，这必将导致空间复杂度极大。

那么如何优化呢？

还是拿上面的爬台阶的例子来说明。根据上面的树状图示，显然每次求当前层的函数值时，只会用到紧邻的下一层的几个函数值，这意味着更深层的函数值都没有用了，可以舍去、释放内存。

换言之，无论是使用“备忘录法”还是“动态规划”，都要分析状态转移函数，看看“降维”前后到底涉及哪些状态，不在这个状态集合里的函数值都可以舍去、释放内存。