一、八皇后问题介绍
八皇后问题,是一个古老而著名的问题,是 回溯算法的典型案例 。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即: 任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法 。

二、八皇后问题算法思路分析
(1)第一个皇后先放第一行第一列
(2)第二个皇后放在第二行第一列、然后判断是否OK,如果不OK,继续放在第二列、第三列、依次把所有列都放完,找到一个合适的
(3)继续第三个皇后,还是第一列、第二列......直到第8个皇后也能放在一个不冲突的位置,算是找到了一个正确解
(4)当得到一个正确解时,在栈回退到上一个栈时,就会开始回溯,即将第一个皇后,放到第一列的所有正确解,全部得到。
(5)然后回头继续第一个皇后放第二列,后面继续循环执行1,2,3,4的步骤
示意图:

说明:
理论上应该创建一个二维数组来表示棋盘,但是实际上可以通过算法,用一个一维数组即可解决问题。arr[8]={0,4,7,5,2,6,1,3}//对应arr下标 表示第几行,即第几个皇后,arr[i]=val,val表示第i+1个皇后,放在第i+1行的第val+1列
代码
public class Queue8 {
//定义一个max表示共有多少个皇后
int max=8;
//定义一个数组array,保存皇后位置的结果,比如 arr={0,4,7,5,2,6,1,3}
int[] array= new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法",count);
System.out.printf("一共判断冲突的次数%d次",judgeCount);
}
//编写一个方法,放置第n个皇后
//特别注意:check 是 每一次递归时,进入到check中都有 for(int i=0;i<max;i++),因此会有回溯
private void check(int n){
if(n==max){//n=8,其实8个皇后已经放好
print();
return;
}
//依次放入皇后,并判断是否冲突
for(int i=0;i<max;i++){
//先把当前这个皇后n,放到改行的第1列
array[n]=i;
//判断当放置第n个皇后到i列时,是否冲突
if(judge(n)){//不冲突
//接着放n+1个皇后,即开始递归
check(n+1);
}
//如果冲突,就继续执行array[n]=i;即将第n个皇后,放置在本行的后移的一个位置
}
}
//查看当前我们放置的第n个皇后,就去检测该皇后是否和前面已经摆放的皇后冲突
/**
* @param n:表示第几个皇后
* */
private boolean judge(int n){
judgeCount++;
for(int i=0;i<n;i++){
//1.array[i]==array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2.Math.abs(n-i) == Math.abs(array[n]-array[i] 表示判断第n个皇后是否和第i皇后是否在同意斜线上
//n=1 放置第2列 1 n = 1 array[1]=1
//Math.abs(1-0) == 1 Math.abs(array[n]-array[i]=Math.abs(1-0)=1)
//3.判断是否在同一行,没有必要,n每次都在递增
if(array[i]==array[n]||Math.abs(n-i) == Math.abs(array[n]-array[i])){
return false;
}
}
return true;
}
//输出皇后摆放的位置
private void print(){
count++;
for(int i=0;i<array.length;i++){
System.out.print(array[i]+" ");
}
System.out.println();
}
}
运行结果
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4
1 4 6 0 2 7 5 3
1 4 6 3 0 7 5 2
1 5 0 6 3 7 2 4
1 5 7 2 0 3 6 4
1 6 2 5 7 4 0 3
1 6 4 7 0 3 5 2
1 7 5 0 2 4 6 3
2 0 6 4 7 1 3 5
2 4 1 7 0 6 3 5
2 4 1 7 5 3 6 0
2 4 6 0 3 1 7 5
2 4 7 3 0 6 1 5
2 5 1 4 7 0 6 3
2 5 1 6 0 3 7 4
2 5 1 6 4 0 7 3
2 5 3 0 7 4 6 1
2 5 3 1 7 4 6 0
2 5 7 0 3 6 4 1
2 5 7 0 4 6 1 3
2 5 7 1 3 0 6 4
2 6 1 7 4 0 3 5
2 6 1 7 5 3 0 4
2 7 3 6 0 5 1 4
3 0 4 7 1 6 2 5
3 0 4 7 5 2 6 1
3 1 4 7 5 0 2 6
3 1 6 2 5 7 0 4
3 1 6 2 5 7 4 0
3 1 6 4 0 7 5 2
3 1 7 4 6 0 2 5
3 1 7 5 0 2 4 6
3 5 0 4 1 7 2 6
3 5 7 1 6 0 2 4
3 5 7 2 0 6 4 1
3 6 0 7 4 1 5 2
3 6 2 7 1 4 0 5
3 6 4 1 5 0 2 7
3 6 4 2 0 5 7 1
3 7 0 2 5 1 6 4
3 7 0 4 6 1 5 2
3 7 4 2 0 6 1 5
4 0 3 5 7 1 6 2
4 0 7 3 1 6 2 5
4 0 7 5 2 6 1 3
4 1 3 5 7 2 0 6
4 1 3 6 2 7 5 0
4 1 5 0 6 3 7 2
4 1 7 0 3 6 2 5
4 2 0 5 7 1 3 6
4 2 0 6 1 7 5 3
4 2 7 3 6 0 5 1
4 6 0 2 7 5 3 1
4 6 0 3 1 7 5 2
4 6 1 3 7 0 2 5
4 6 1 5 2 0 3 7
4 6 1 5 2 0 7 3
4 6 3 0 2 7 5 1
4 7 3 0 2 5 1 6
4 7 3 0 6 1 5 2
5 0 4 1 7 2 6 3
5 1 6 0 2 4 7 3
5 1 6 0 3 7 4 2
5 2 0 6 4 7 1 3
5 2 0 7 3 1 6 4
5 2 0 7 4 1 3 6
5 2 4 6 0 3 1 7
5 2 4 7 0 3 1 6
5 2 6 1 3 7 0 4
5 2 6 1 7 4 0 3
5 2 6 3 0 7 1 4
5 3 0 4 7 1 6 2
5 3 1 7 4 6 0 2
5 3 6 0 2 4 1 7
5 3 6 0 7 1 4 2
5 7 1 3 0 6 4 2
6 0 2 7 5 3 1 4
6 1 3 0 7 4 2 5
6 1 5 2 0 3 7 4
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
一共有92解法一共判断冲突的次数15720次
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
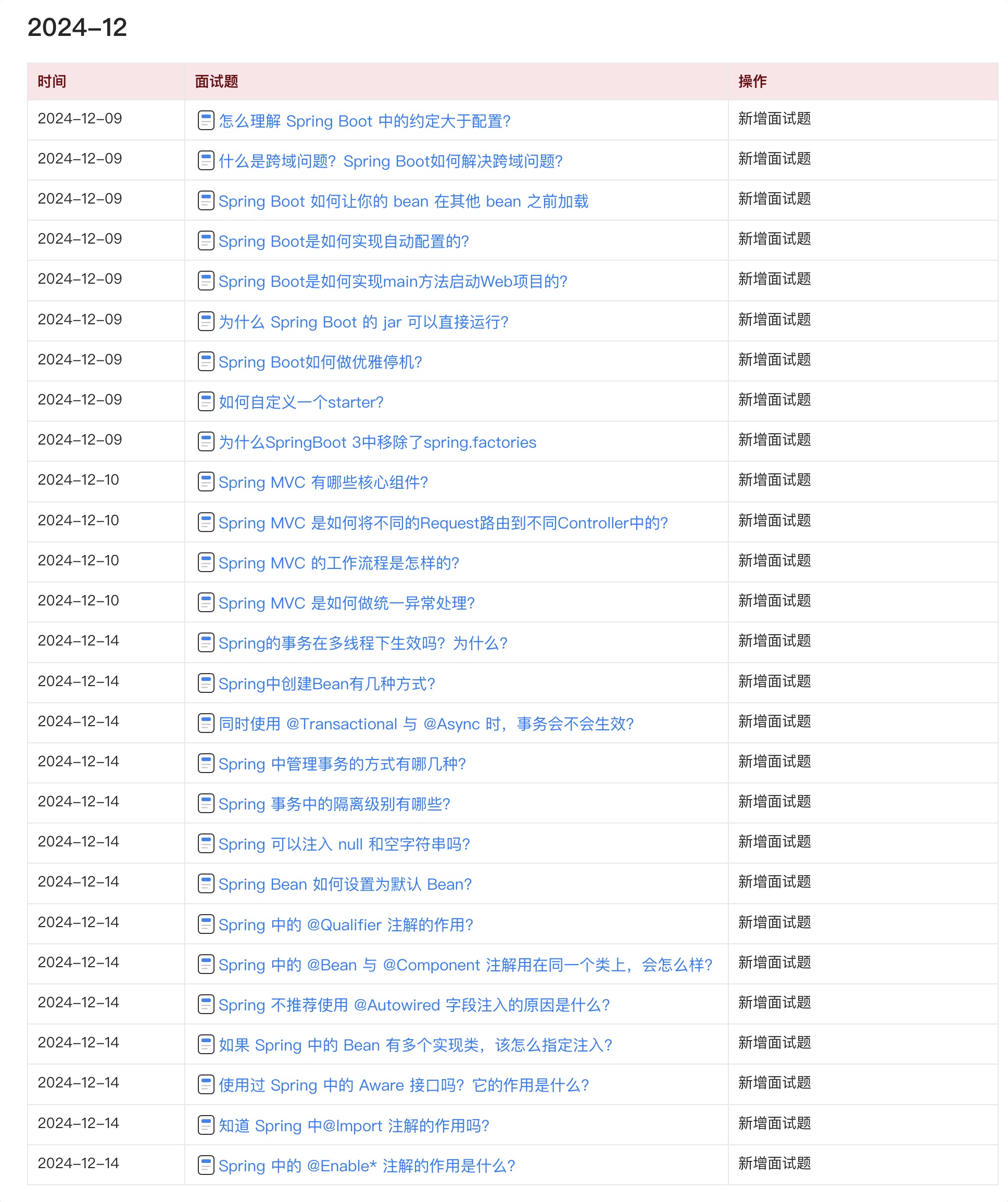
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

