引言
在上一篇《无死角“盘”它!二分查找树》中提到了:平衡二叉树的目的就是使得平均查找长度最短。那么这里就引出两个问题:
- 什么是平衡二叉树?
- 为什么平衡二叉树的平均查找长度最短?
- 如何将非平衡二叉树调整成平衡二叉树?
1. 平衡二叉树是什么鬼?
满足如下两个条件的二叉树称为“平衡二叉树”:
- 首先它得是二分查找树
- 然后它的左右子树的高度相差不超过1
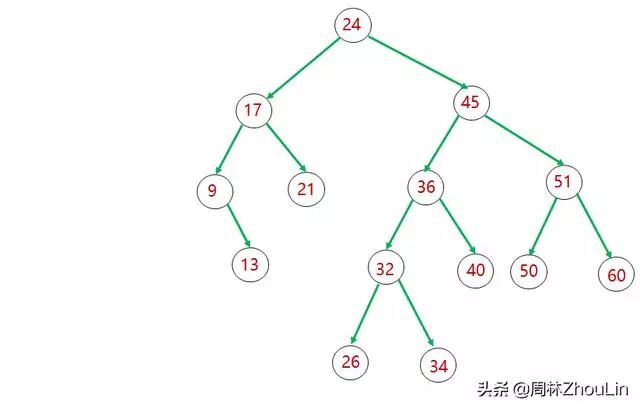

图1 平衡二叉树
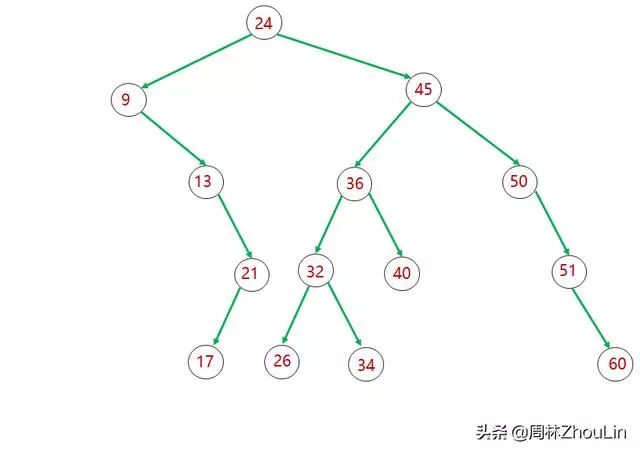

图2 非平衡二叉树
图1就是一棵平衡二叉树,而图2不是平衡二叉树。
在图2中,对于值为9的节点,它的左子树为空,高度为0,右子树高度为3,两者相差3,不满足平衡二叉树定义的第二条规则。
2. 如何证明平衡二叉树的平均查找长度最短?
首先研究一下平衡二叉树与非平衡二叉树的关系。
图3表示的是一棵平衡二叉树,与它对应的任意一棵非平衡二叉树都可以重复按照如下方式变换而来——在维持二分查找树的前提下,从高度较小的子树中取出一个节点A,插入到高度较大的子树中——如图4所示。
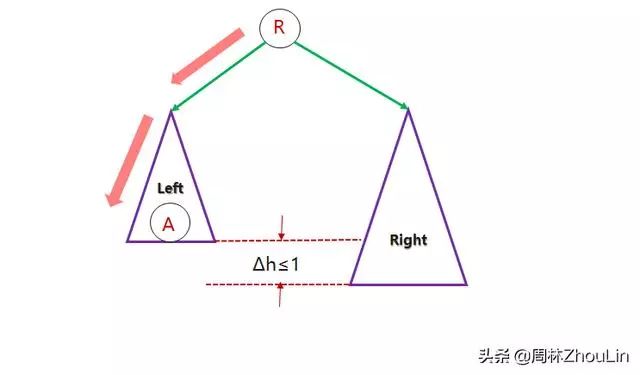

图3 平衡二叉树与非平衡二叉树的转换
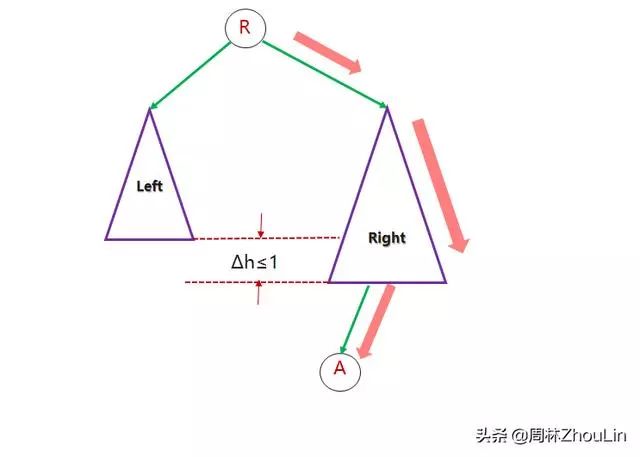

图4 平衡二叉树与非平衡二叉树的转换
接下来用反证法来证明:
假设平衡二叉树的平均查找长度L并不是最短的,那么必然存在一棵非平衡二叉树的平均查找长度L'<L (命题1)
对应到上面的图示就是:
图3的平衡二叉树的平均查找长度L>图4的非平衡二叉树的平均查找长度L’(假设1)
假设1其实是命题1的充分条件,也就是说:只要假设1为真,命题1必为真。
图3的节点总数=图4的节点总数,设为N;
设节点A在图3中的查找长度(从根节点到A所需要的比较次数)为La,在图4中的查找长度为La’,则根据平均查查长度的定义
平均查找长度=每个节点的查找长度之和/节点总数
得到:
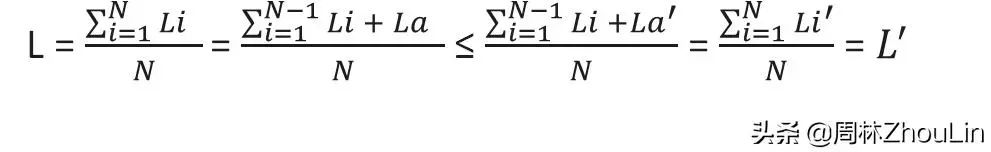

显然上式与前面的假设1矛盾,从而证明了平衡二叉树的平均查找长度最短。
3. 如何将非平衡二叉树调整成平衡二叉树?
朴素的想法就是:遍历每个节点,检查它的左右子树高度,若高度之差超过1,设法交换一些节点的位置,使得该位置左右子树新的高度差缩减到1以内。
这里牵扯出3个问题:
- 遍历的方向:自顶向下还是自底向上?
- 遍历的时候如何方便地获取左右子树的高度?
- 如何交换节点的位置,使得新的高度差在1以内?
对于问题1,如果你仔细研究过笔者前几篇文章的话——《神力加身!动态编程》《史上最猛之递归屠龙奥义》——那么你很容易得出结论:
两个方向都可以:自顶向上的话,写递归式算法;自底向上的话,写非递归式算法。
这里的“顶”指的是二叉树的根节点,“底”指的是二叉树的尾节点。
对于问题2,取决于问题1采用哪种方式——如果采用递归式算法,那么在递归的时候,也顺便把高度递归计算了;如果采用非递归式,那么就在自底向上归并的时候,动态计算高度。
问题3才是真正的新鲜问题。图5和图6分别描述了一般情况。
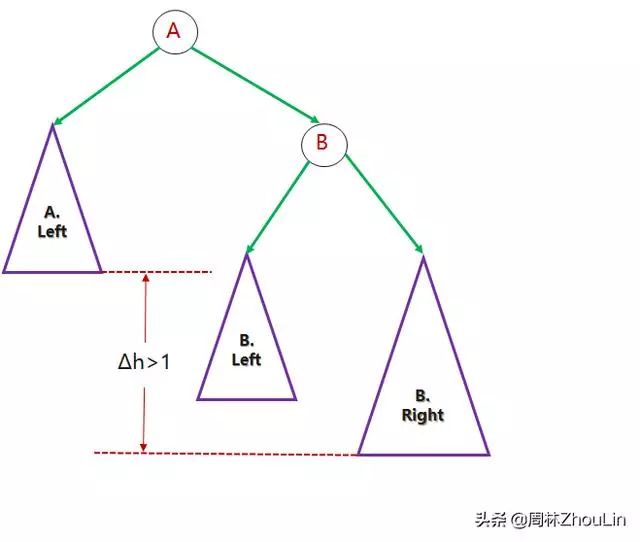

图5
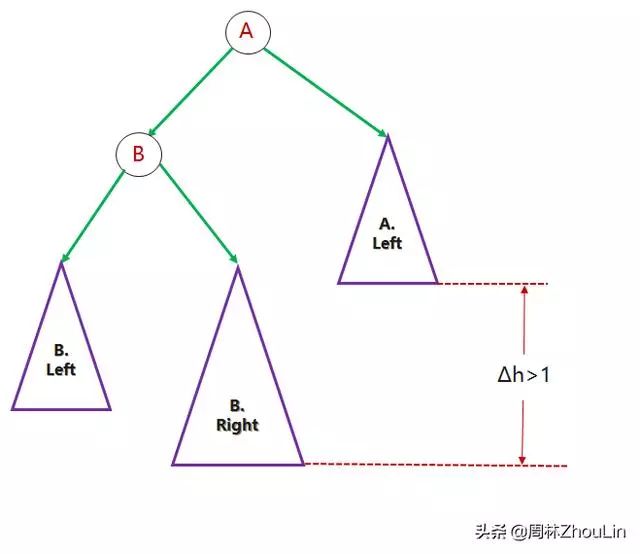

图6
为了解决这个“新鲜问题”,我们先来看一个引理:
引理12.1
- 因为任意非叶子节点A,它的值都比其右孩子B的值小,所以它可以变成B的左孩子。这样变换之后,A、A的左子树下降,B、B的右子树上升,高度差变小。
- 因为任意非叶子节点A,它的值都比其左孩子C的值大,所以它可以变成C的右孩子。这样变换之后,A、A的右子树下降,B、B的左子树上升,高度差变小。
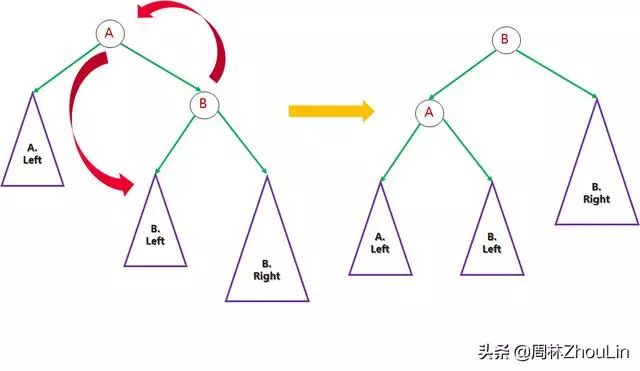

图7
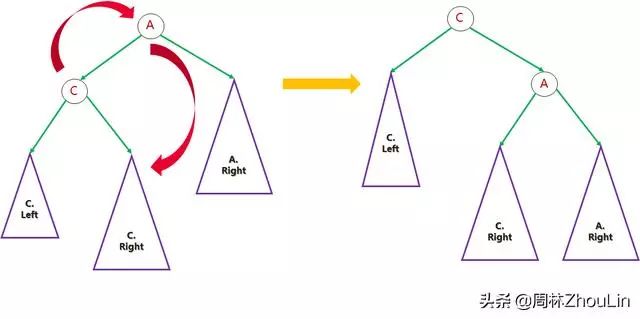

图8
上述的变换是不是很像一种“旋转”:)
那么是不是这样“旋转”之后,调整就OK了呢?答案是否定的。
看看下面这个例子:
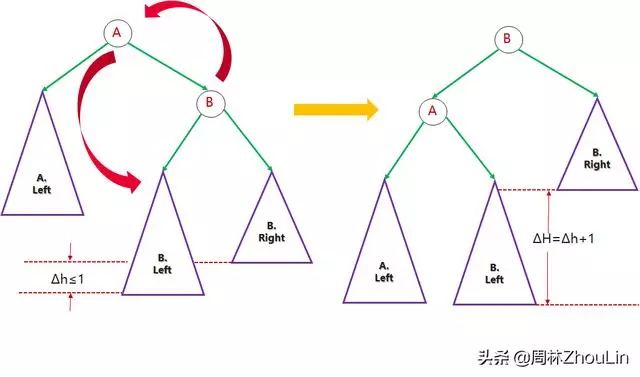

图9
图9中,B节点一开始的左子树高度比其右子树大,即:
H(B.Left)=H(B.Right)+∆h (式1)
“旋转”调整后,B的左子树变成A的右子树,A变成B的左孩子,设高度相对于节点的函数为H,则:
H(A)=Max(H(B.Left), H(A.Left))+1
≥H(B.Left)+1 (式2)
将式1代入式2可得:
H(A)≥H(B.Right)+∆h+1
=H(B.Right)+∆H (式3)
当∆h=1时,∆H=2。
此时H(A)≥H(B.Right)+2,这意味着“旋转”后,B节点的左子树高度与右子树高度相差超过1!
貌似“旋转”对这种情况不凑效了,怎么办呢?
先来分析一下不凑效的根因到底是什么。
从图9可以看出,作为A节点的右孩子,从一开始,B节点的左子树就比其右子树高了一个头,这个是导致后面旋转不凑效的根因。所以很自然地想到:
在旋转前,先把B节点的左子树高度降低或者把右子树高度升高。
那么如何实现上述目标呢?我们能利用的仍然是引理12.1:
先将B节点的左子树展开
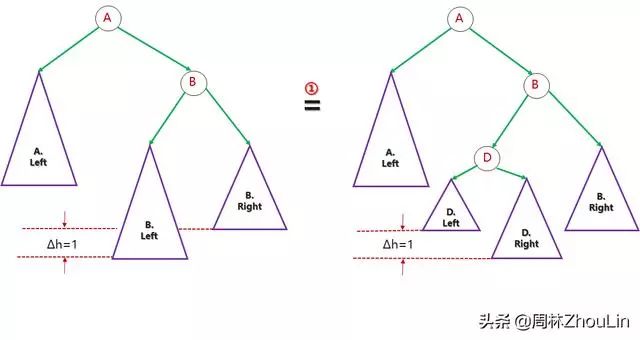

图10
再对展开的子树做一次旋转:
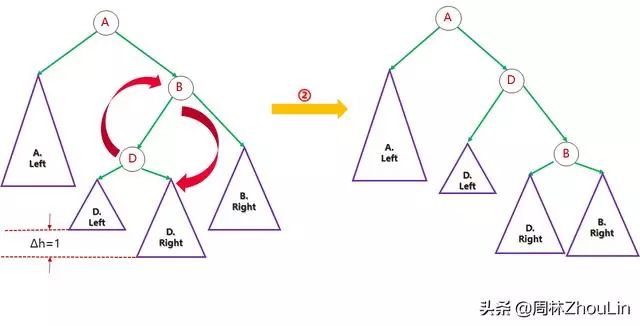

图11
通过以上两步就达成了把原始B节点位置(现在是D节点)的左子树高度降低的目的。
至此就转换成了熟悉的老问题。再做一次旋转便可以彻底调整成平衡二叉树了:
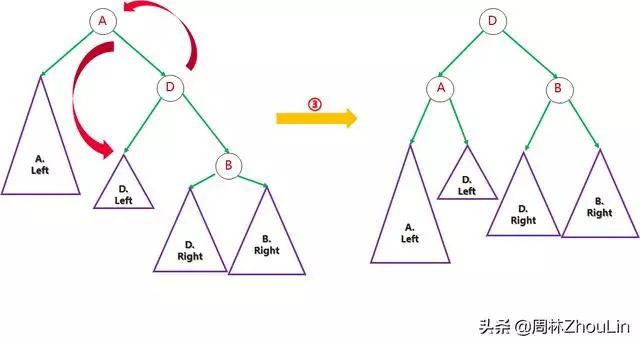

图12
对称地,我们可以用类似的步骤来调整下图的非平衡二叉树:
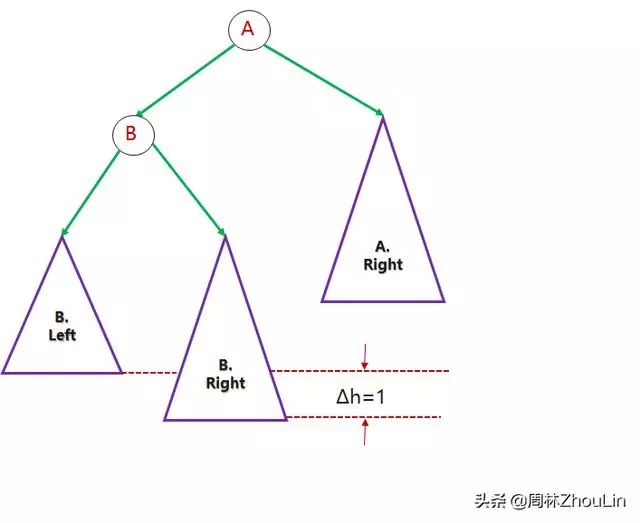

图13
步骤一(子树展开):
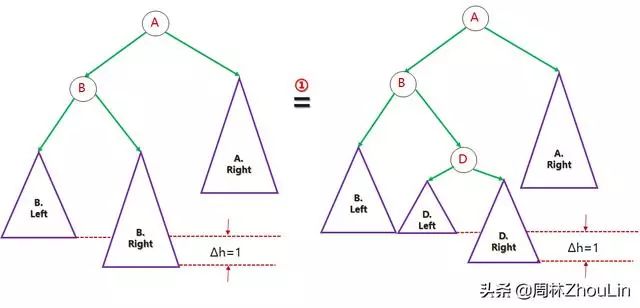

图14
步骤二(一次旋转):
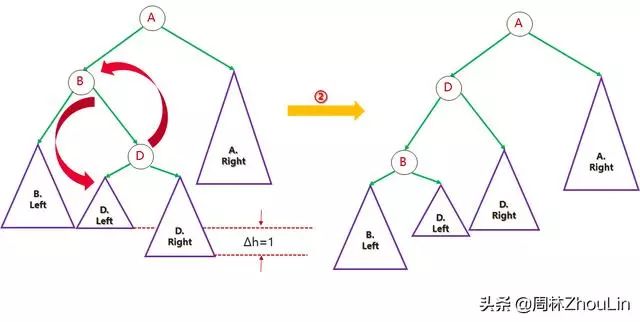

图15
步骤三(二次旋转):
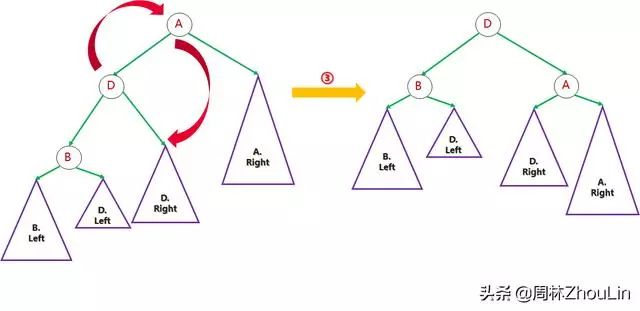

图16
综上所述,自顶向下的、单向链表存储式、递归型平衡二叉树调整算法如下:


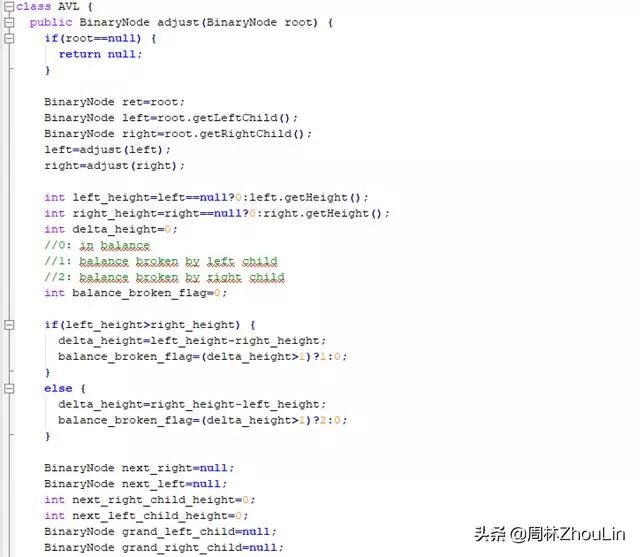

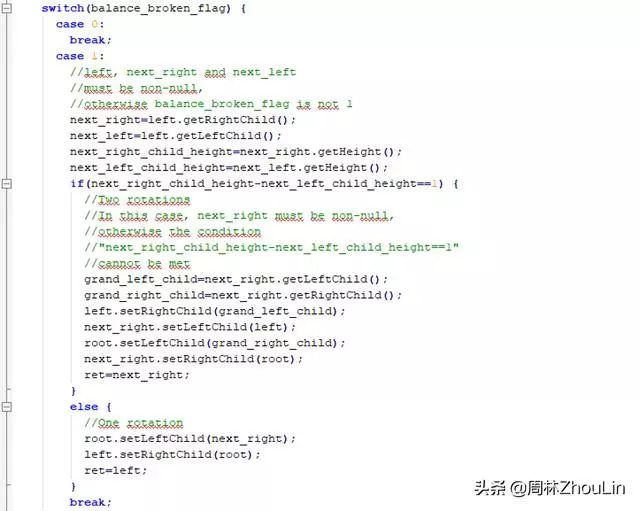

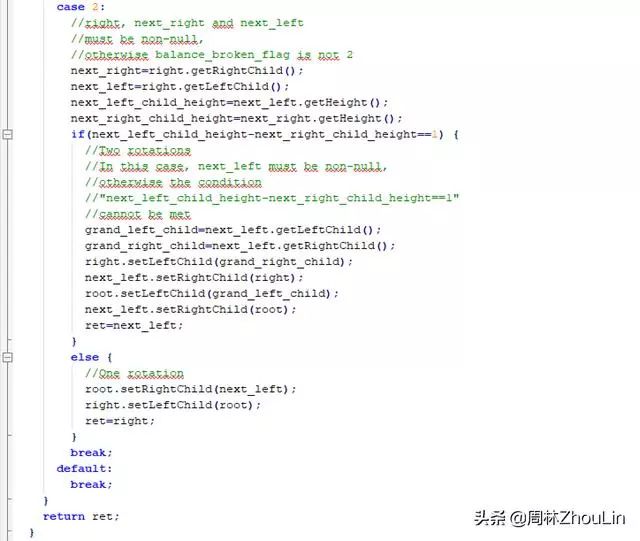

为了节省篇幅,自底向上的、单向链表存储式、非递归型平衡二叉树调整算法和自底向上的、数组存储式、非递归型平衡二叉树调整算法放在下一篇文章里单独列示。
4. 平衡二叉树的节点插入算法
首先平衡二叉树本质是二分查找树,所以插入新节点时,可遵循《无死角“盘”它!二分查找树》中的节点插入算法;
但是平衡二叉树还是特殊的二分查找树,它还要满足左右子树高度相差不超过1的要求。当按照上面的算法插入新节点之后,可能会不满足这个要求,因此要进行调整。调整算法仍然是章节3介绍的旋转调整算法。
5. 平衡二叉树的节点删除算法
首先平衡二叉树本质是二分查找树,所以删除节点时,可遵循《无死角“盘”它!二分查找树》中的节点删除算法;
但是平衡二叉树还是特殊的二分查找树,它还要满足左右子树高度相差不超过1的要求。当按照上面的算法删除节点之后,可能会不满足这个要求,因此要进行调整。调整算法仍然是章节3介绍的旋转调整算法。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

