引言
二叉树的叶子节点的孩子都是空节点(Null),如果展开显示,如下图:


图 1 原始二叉树
二叉树的遍历方法,有“前序遍历”“中序遍历”和“后序遍历”三种。
“前序遍历”的规则:
- 先访问当前节点,再访问其左子树,最后访问右子树;
- 访问子树时,按照规则1递归执行。
“中序遍历”的规则:
- 先访问左子树,再访问当前节点,最后访问右子树;
- 访问子树时,按照规则1递归执行。
“后序遍历”的规则:
- 先访问左子树、再访问右子树,最后访问当前节点;
- 访问子树时,按照规则1递归执行。
如果要写出非递归的遍历算法,无论用哪种遍历方法,根据《再不会“降维打击”你就Out了!》《神力加身!动态编程》三篇文章中讲到的知识和技巧,都要借助堆栈来记忆“历史路径”以用于回溯。此方法是经典做法,但同时也有两个显著弊端:
- 堆栈需要额外的存储;
- 额外需要的存储带来的空间复杂度也不是O(1)型的——是与节点总数动态相关。
那么是否存在能找到一种技巧来解决上述的弊端呢?
今天就来介绍一种“奇技淫巧”——线索二叉树——来搞定这个问题:)
什么是线索二叉树?
严格意义上的线索二叉树定义如下:
一个二叉树通过如下的方法“穿起来”:所有原本为空的右(孩子)指针改为指向该节点在中序序列中的后继,所有原本为空的左(孩子)指针改为指向该节点的中序序列的前驱。
本文为了追求更直观、更快速的算法效果,对上述传统线索二叉树做了如下改良:
- 不同的遍历方法,对应的线索二叉树不同;
- 尽可能只利用后继节点。
这里先以“中序遍历”对应的线索二叉树为例。
“中序遍历”的线索二叉树说白了,就是两条规则:
- 将当前节点左子树中的最右叶子节点的右孩子指针指向当前节点本身;
- 对每个节点,递归执行规则1。
规则1看起来比较绕,用一张图来表示:


图2 “中序遍历”的线索二叉树
图2就是图1对应的“中序遍历”的线索二叉树。
线索二叉树的意义
传统的非递归型遍历算法,最挑战的地方在于要记忆“回溯点”。
以“中序遍历”为例,它要先访问当前节点的左子树之后,再访问当前节点——这意味着,访问完左子树前,先要记住当前节点位置;否则,访问完左子树之后,就找不到返回位置了。经典做法是通过堆栈来记忆。如果不想引入额外存储,那么怎么“记住”呢?
对比图2和图1,可以看出:“中序遍历”的线索二叉树其实就是复用了指向“空节点”的指针!——它将当前节点左子树的最右叶子节点的右孩子指针(原来指向“空节点”),指向了当前节点!
至于“前序遍历”的线索二叉树,就是将当前节点左子树的最右叶子节点的右孩子指针(原来指向“空节点”),指向当前节点的直接右孩子:


图3 “前序遍历”的线索二叉树
至于“后序遍历”的线索二叉树,就复杂了:
- 仅仅利用叶子节点的指针,解决不了所有后继节点的寻址;
- 非叶子节点的孩子指针无法直接复用,若用于指示后继节点,会丢失本来的孩子节点的链接。
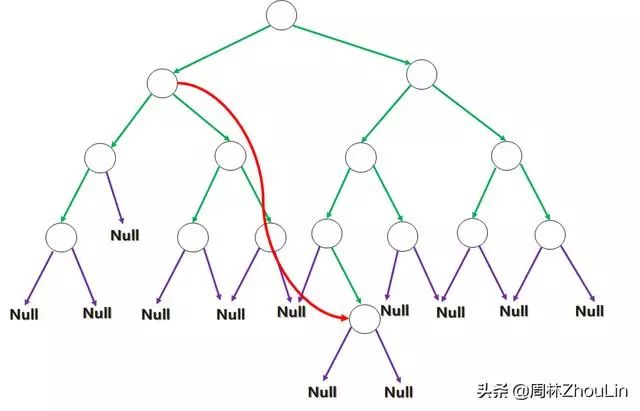

图4 “后序遍历”的线索二叉树构造问题
解决上述困难,有两种途径:
- 利用其它遍历方法的线索二叉树来做“后序遍历”;
- 对原始二叉树做结构改造,以符合前驱或者后继寻址的需要。
如何将二叉树转换成线索二叉树?
为了节省篇幅,本文仅介绍“中序遍历”的线索二叉树的转换以及遍历算法。
构造线索二叉树的目的,说到底还是为了遍历。那么这就引出一个现实问题:
到底是构造完线索二叉树之后,再启动遍历呢?还是边构造边遍历呢?
从上面的线索二叉树的定义就可以看出,为了复用“空节点”指针,需要访问叶子节点,这个已经是遍历的一部分了,所以为了“不走重复路”,最经济的方法是边构造边遍历。
递归型“中序遍历”的线索二叉树的转换以及遍历算法:


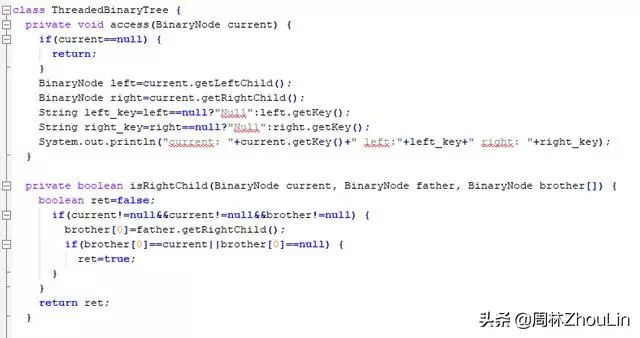





非递归型“中序遍历”的线索二叉树的转换以及遍历算法:




后记:
接下来的文章将分别介绍“前序遍历”的线索二叉树的各种转换以及遍历算法、“后序遍历”的线索二叉树的各种转换以及遍历算法。
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
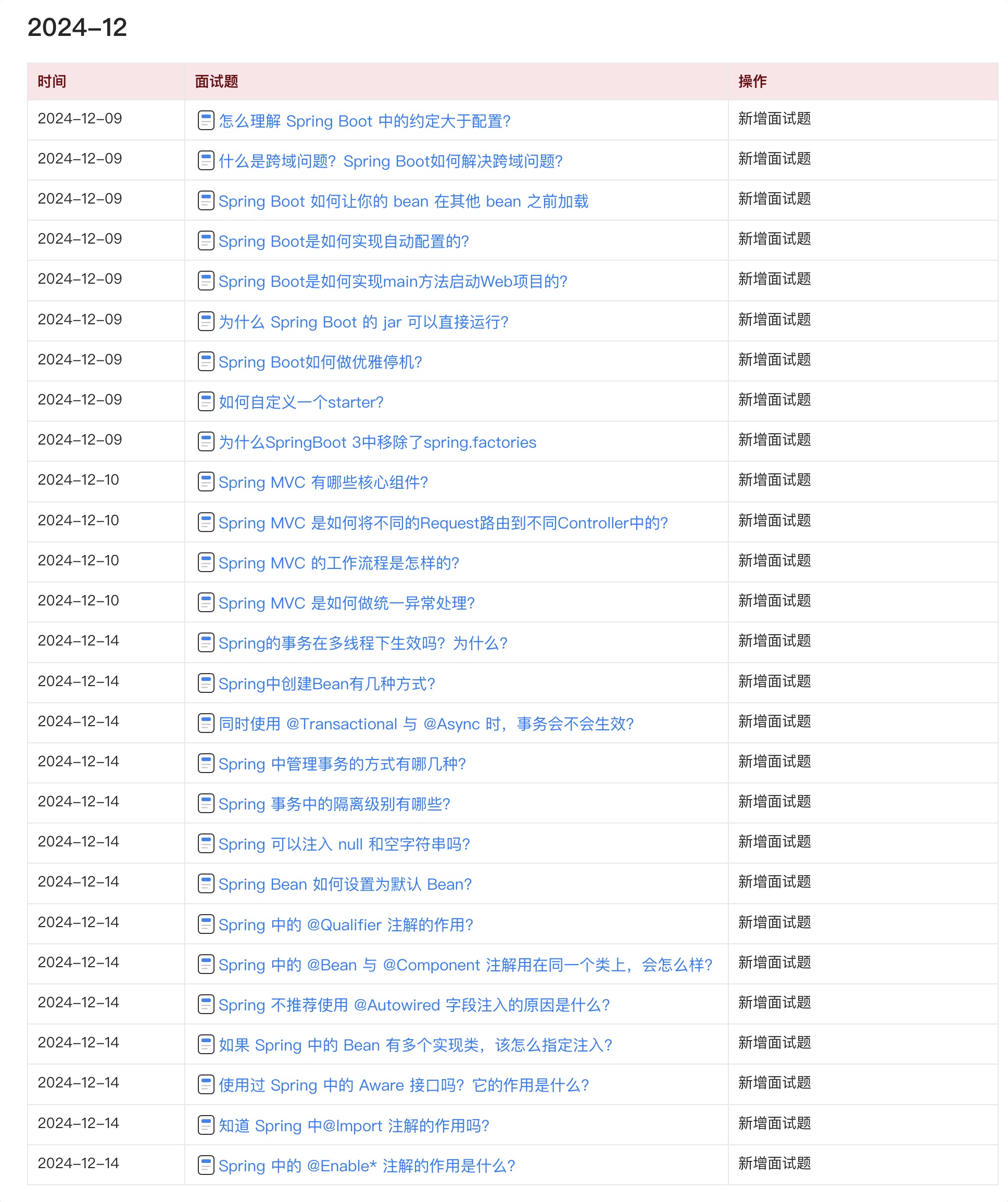
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

