引言
刘慈欣的《三体》不仅让中国的硬科幻登上了世界的舞台，更是给广大读者普及了诸如“降维打击”之类的热门概念。
“降维打击”之所以给人如此之震撼，在于它以极简的方式，从更高的、全新的技术视角有效解决了当前困局。
那么在算法的世界中，是否存在这样的利器呢？答案是肯定的——那就是大名鼎鼎的“递归”。
递归思想与传统算法思想的区别
传统算法思想是正向演绎逻辑，即：根据已知条件，进行联想、寻找经验库，逐步推导，直到问题解决。
而递归思想是逆向归纳逻辑，即：当前问题的求解是否可以由规模小一点的问题求解叠加而来，后者是否可以再由更小一点的问题求解叠加而来……依此类推，直到收敛为一个极简的出口问题的求解。
由上可知，递归的本质借鉴的就是数学归纳法：
证明一个与自然数n有关的命题S(n），若：
（1）可证明当n取第一个值n1时命题成立；
（2）假设当n=k（k>=n1，k为自然数）时命题成立，可证明当n=k+1时命题也成立。
那么综合（1）（2），对一切自然数n（n>=n1），命题S(n）都成立。
把上面数学归纳法定义中的“证明”换成“求解”，就是递归思想：）
数学归纳法的一个直观理解就是“多米诺骨牌”：
只要推倒第一张骨牌（解决出口问题），那么后面的骨牌（规模逐次升高的问题）就依次倒下（被解决）。
递归思想的优势
说了半天递归思想的意义，那么它到底在实操时有什么优势呢？
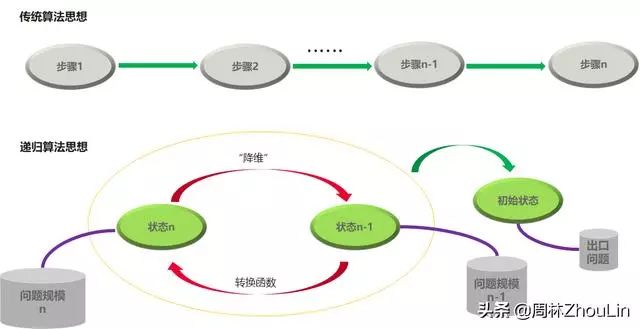
由上图可知：
-
传统算法是以“步骤”为中心的、递归算法是以“状态/规模”为中心的；
-
传统算法必须有步骤序列的全景图，才能解决问题；递归算法只要有“状态转移函数”和初始状态/出口问题的解，就能解决问题；
-
针对当前问题，如果很难直接推导出完整的步骤序列，那么传统算法是很难凑效的。
换言之，递归算法将面向过程的求解思路转换成面向状态机的求解思路。
而计算机本质就是一个状态机，这个天然的性质决定了递归算法更适合计算机“理解”、求解。
递归应用的初步套路
第一步：识别规模因子
第二步：识别初始状态和出口问题，求对应的解
第三步：识别状态转移条件、抽象状态转移函数
现有一个级数为n的台阶，每次你可以爬1,2或者3级台阶，请问爬完整个n级台阶有多少种方法？
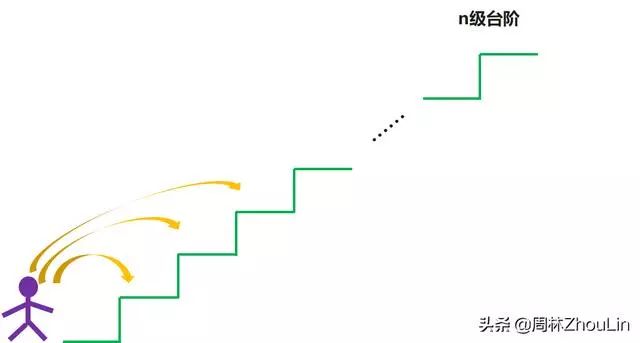
解答：
第一步：识别规模因子。
规模因子说白了就是个变量，首先在题目中找变量。
显然，题目中变量由两个：一个是台阶的级数，一个是每次爬的台阶数
那么哪个变量是规模因子呢？
判定规模因子的方法：变量的取值范围是否是未知的、是否范围是很大的？
每次爬的台阶数的取值范围是1,2,3，是确定的；台阶的级数的取值范围是不确定的。
所以规模因子是台阶的级数。
第二步：识别初始状态和出口问题，求对应的解。
初始状态就是规模因子缩小到最小时的状态。
出口问题包含初始状态对应的问题和边界问题。
在本题中，显然规模因子最小的状态就是台阶的级数为1的状态，此时显然种数为1（爬1级到到第1级台阶）
边界问题指的是当规模因子非正常取值的时候的问题形态。
在本题中，显然台阶数如果取0或者负值，是非正常取值，这个时候的问题形态就是边界问题。
显然在这样的场景下，是无解的，即：方法的种数是0
第三步：识别状态转移条件、抽象状态转移函数。
按照上面递归思想的图示，求状态转移函数，就是构造规模n-1的解映射到规模n的解的函数。
针对本题：
规模n-1就对应n-1级台阶；规模n-1的解就是爬到第n-1级台阶的方法种数。
规模n就对应n级台阶；规模n的解就是爬到第n级台阶的方法种数。
而从第n-1级台阶爬到第n级台阶，就只有一种方法，向上爬1步。根据排列组合的乘法原理：
f(n)=f(n-1) x 1，即：f(n)=f(n-1)
看上去，我们已经按照套路“完美”解决了这个问题。但真的是这样吗？
细心的你，肯定发现了：
由于每次爬台阶可以爬1,2或者3步，但是上面的转移函数只考虑了爬1步的情况！
很容易看出，问题的根因来自上面递归思想的图示！
其实，上面的递归思想的图示只描述了递归思想的核心，是个简化版；
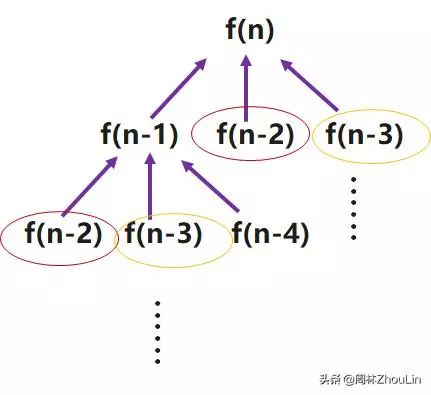
更一般的正确形式是下图所示：
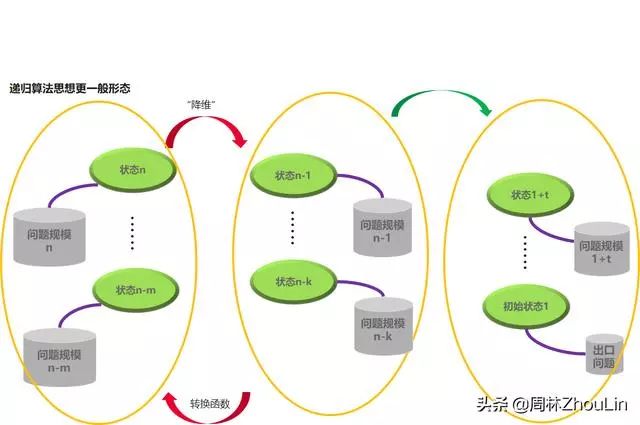
稍稍比较一下两张图就可以看出：
区别在于降维时的状态单一性。
在简化版图示中，降维前后的状态是单一的；而在一般版图示中，降维前后是多个状态的组合！
回到本题，如果应用上面的一般版图示，那么降维前的状态就是台阶数为n的情况，降维后的状态就是台阶数分别为n-1, n-2和n-3这3种情况的组合。
1. f(n-1) -> f(n):
从第n-1级台阶到第n级台阶只有1种爬法
根据排列组合的乘法原理 =>f(n)=f(n-1)x1 （式1）
2. f(n-2) -> f(n):
从第n-2级台阶到第n级台阶有2种爬法：
第1种：直接爬2级到第n级
根据排列组合的乘法原理 =>此时f(n)=f(n-2) x 1
第2种：先爬1级，变成f(n-1)的情况，再叠加f(n-1)的解
显然该情况包含在f(n-1)的所有情况中，忽略、不做重复计算
所以根据排列组合的加法原理，整体：
f>f(n)=f(n-2)x1 （式2）
3. f(n-3) -> f(n):
从第n-3级台阶到第n级台阶有3种爬法：
第1种：直接爬3级到第n级
根据排列组合的乘法原理 =>此时f(n)=f(n-3) x 1
第2种：先爬1级，变成f(n-2)的情况，再叠加f(n-2)的解
同上，显然该情况包含在f(n-2)的所有情况中，忽略、不做重复计算
第2种：先爬2级，变成f(n-1)的情况，再叠加f(n-1)的解
同上，显然该情况包含在f(n-1)的所有情况中，忽略、不做重复计算
f()中的变量的正常取值>=1，从而有n-3>=1 => n>=4
且根据排列组合的加法原理 =>f(n)=f(n-3)x1（式3）
根据排列组合的加法原理、综合式1、式2、式3，得到：
当n>=4时：
f(n)=f(n-1)+f(n-2)+f(n-3) （式4）
我们在第一步时，只求了初始状态n=1的解：
f(1)=1 （式5）
根据（式4）和上面的一般版图示，我们还得求n=2,3时的解。
对于n=2有以下情况：
- 初始状态问题转移：
f(1) -> f(2):
从第1级台阶到第2级台阶只有1种爬法
根据排列组合的乘法原理 =>f(2)=f(1)x1 （式6）
- 边界问题转移：
f(0) -> f(2):
从第0级台阶到第2级台阶有2种爬法：
第1种：直接爬2级到第2级
注意：对于边界问题，不能直接应用排列组合的乘法原理，否则恒等于0！
此时要省去边界解作为乘法因子！
换言之，对于当前这种情况，不能写成f(2) = f(0) x 1，要写成
f(2) = 1
第2种：先爬1级，变成f(1)的情况，再叠加f(1)的解
显然该情况包含在f(1)的所有情况中，忽略、不做重复计算
所以根据排列组合的加法原理，整体：f(2)=f(1)x1+1=1x1+1=2 （式8）
同理，可求得：f(3)=3 （式9）
综合式4、式5、式8、式9，得到最终的递归算法：>当n>=4时：
f(n)=f(n-1)+f(n-2)+f(n-3）
当1<=n<4时：f(n)=n
当n<1时：f(n)=0
递归应用的优化套路
从上面的例子可以看出，在实操中使用“递归应用的初步套路”可能会遇到降维后状态非单一问题，该问题会导致必须扩展初始状态/边界问题的集合。
扩展的集合的大小取决于通用状态转移函数的定义域与初始状态之差。
上面的例子中，通用状态转移函数的定义域是n>=4，初始状态是n=1，所以扩展范围是n=2和n=3。
由此，我们可以得到递归应用的优化套路：
第一步：识别规模因子
第二步：识别状态转移条件、抽象状态转移函数
第三步：识别初始状态和边界问题、求函数值
第四步：根据第二步和第三步求出扩展集合
第五步：对扩展集合中的元素逐一求函数值
第六步：综合第二步、第三步、第五步的结果
进一步思考的话，可以看出：
扩展集合实际上对应的就是通用状态转移函数失效的取值范围。
状态转移函数降级的话，就可以缩小扩展集合的大小。不断降级，就可以不断逼近初始状态。
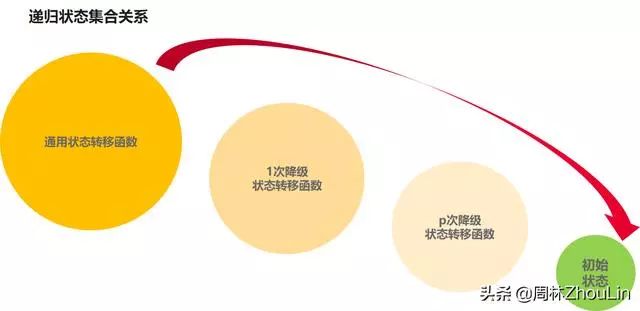
上面的例子中，f(2) = f(1) x 1 + 1就是f(n) = f(n-1)，它实际上就是
f(n) = f(n-1) + f(n-2) + f(n-3)
的降级形式——f(n-2)和f(n-3)去掉就转换成了f(n) = f(n-1)——其失效的取值范围就是n=2和n=3。
递归算法的局限性
从递归算法思想一般版图示可以看出：
局限性1（适用性问题）：
如果“降维”前的状态集合并不方便用“降维”后的状态集合表示，即状态转移函数不好求，那么该场景使用递归不一定恰当。
局限性2（重复计算问题）：
在直接递归的过程中部分函数值会被重复计算。
那么如何解决上面两个问题呢？答案就是“动态编程”。
下篇文章我们就来详细谈谈“动态编程”。
