一、二叉树
1.1 为什么需要树这种数据结构
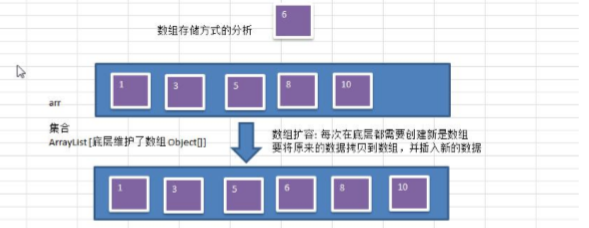
(1)数组存储方式的分析
优点:通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。
缺点:如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低
画出操作示意图:
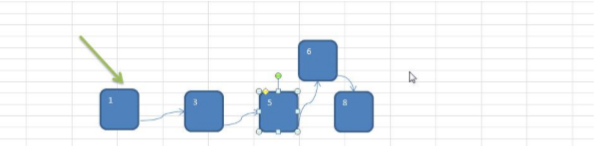
(2)链式存储方式的分析
优点:在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可,删除效率也很好)。
缺点:在进行检索时,效率仍然较低,比如(检索某个值,需要从节点开始遍历)
操作示意图:
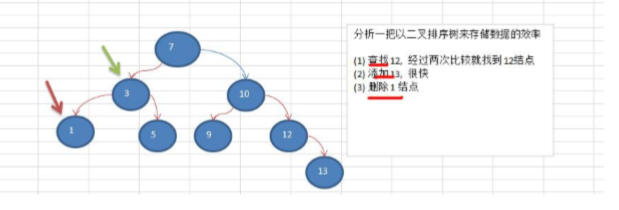
(3)树存储方式的分析
能提高数据存储,读取的效率,比如利用二叉排序树(Binary Sort Tree),即可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度。
案例:【7,3,10,1,5,9,12】
1.2 树示意图
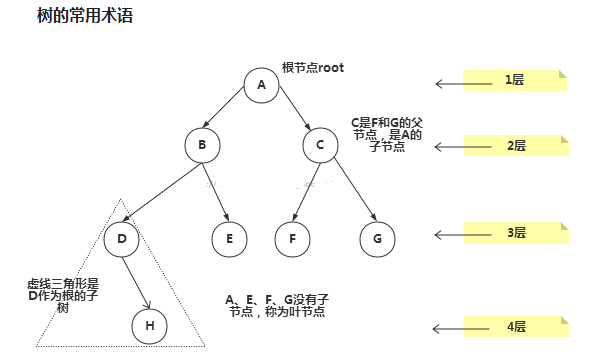
树的常用术语(结合示意图理解): > > 1)节点 > > 2)根节点 > > 3)父节点 > > 4)子节点 > > 5)叶子节点 (没有子节点的节点) > > 6)节点的权(节点值) > > 7)路径(从root节点找到该节点的路线) > > 8)层 > > 9)子树 > > 10)树的高度(最大层数) > > 11)森林 :多颗子树构成森林
1.3 二叉树的概念
(1)树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
(2)二叉树的子节点分为左节点和右节点
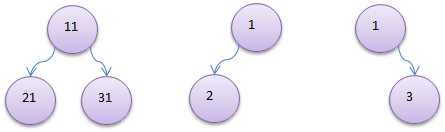
二叉树
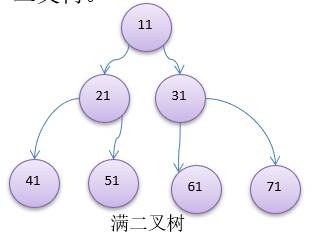
(3)如果该二叉树的所有叶子节点都在最后一层,并且结点总数=2^n-1,n为层数,则我们称为满二叉树。
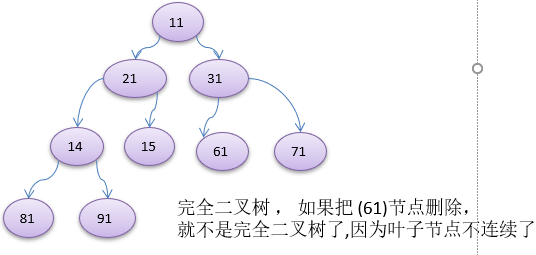
(4)如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连接,倒数第二层的叶子节点在右边连接,我们称为完全二叉树。
1.4 二叉树遍历的说明
使用 前序,中序和后序 对下面的二叉树进行遍历。
前序遍历:先输出父节点,再遍历左子树和右子树
中序遍历:先遍历左子树,再输出父节点,再遍历右子树
后序遍历:先遍历左子树,再遍历右子树,最后输出父节点
**小结:**看输出父节点的顺序,就确定是前序,中序还是后序
Java 面试宝典是大明哥全力打造的 Java 精品面试题,它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题,而是一套完整的 Java 知识体系,一套你 Java 知识点的扫盲贴。
它的内容包括:
- 大厂真题:Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
- 原创内容:Java 面试宝典内容全部都是大明哥原创,内容全面且通俗易懂,回答部分可以直接作为面试回答内容。
- 持续更新:一次购买,永久有效。大明哥会持续更新 3+ 年,累计更新 1000+,宝典会不断迭代更新,保证最新、最全面。
- 覆盖全面:本宝典累计更新 1000+,从 Java 入门到 Java 架构的高频面试题,实现 360° 全覆盖。
- 不止面试:内容包含面试题解析、内容详解、知识扩展,它不仅仅只是一份面试题,更是一套完整的 Java 知识体系。
- 宝典详情:https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
- 宝典总览:https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
- 宝典进展:https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw
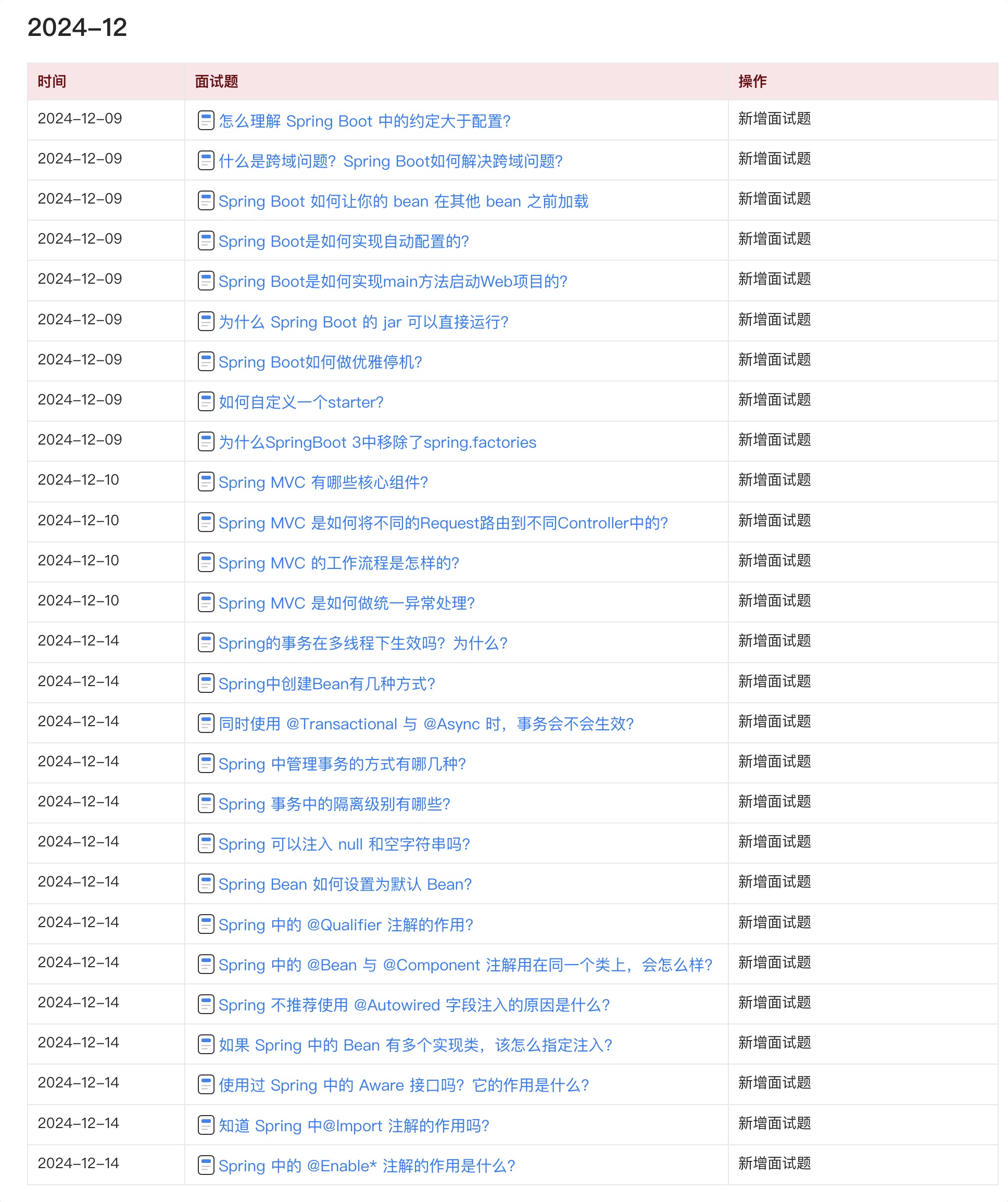
目前 Java 面试宝典累计更新 400+ 道,总字数 42w+。大明哥还在持续更新中,下图是大明哥在 2024-12 月份的更新情况:
想了解详情的小伙伴,扫描下面二维码加大明哥微信【daming091】咨询

同时,大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ,回复【面试题】 即可免费领取。

